题目内容
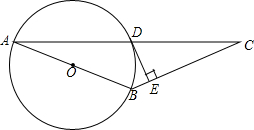 已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.(1)求证:DE为⊙O的切线;
(2)若DE=2,tanC=
| 1 | 2 |
分析:(1)连接OD,利用D是AC中点,O是AB中点,那么OD就是△ABC的中位线,利用三角形中位线定理,可知OD∥BC,而DE⊥BC,则∠DEC=90°,利用平行线的性质,有∠ODE=∠DEC=90°,即DE是⊙O的切线;
(2)连接BD,由于AB是直径,那么∠ADB=90°,即BD⊥AC,在△ABC中,点D是AC中点,于是BD是AC的垂直平分线,那么BA=BC,在Rt△CDE中,DE=2,tanC=
,可求CE=4,再利用勾股定理可求CD=2
,同理在Rt△CDB中,CD=2
,tanC=
,可求BD=
,利用勾股定理可求BC=5,从而可知BA=BC=5.
(2)连接BD,由于AB是直径,那么∠ADB=90°,即BD⊥AC,在△ABC中,点D是AC中点,于是BD是AC的垂直平分线,那么BA=BC,在Rt△CDE中,DE=2,tanC=
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 5 |
解答: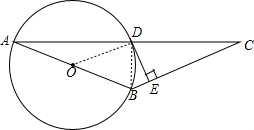 (1)证明:连接OD.
(1)证明:连接OD.
∵D为AC中点,O为AB中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=∠DEC=90°,
∴OD⊥DE于点D,
∴DE为⊙O的切线;
(2)解:连接DB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴DB⊥AC,
∴∠CDB=90°
∵D为AC中点,
∴AB=BC,
在Rt△DEC中,
∵DE=2,tanC=
,
∴EC=
=4,
由勾股定理得:DC=2
,
在Rt△DCB中,BD=DC•tanC=
,
由勾股定理得:BC=5,
∴AB=BC=5,
∴⊙O的直径为5.
 (1)证明:连接OD.
(1)证明:连接OD.∵D为AC中点,O为AB中点,
∴OD为△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴∠DEC=90°,
∴∠ODE=∠DEC=90°,
∴OD⊥DE于点D,
∴DE为⊙O的切线;
(2)解:连接DB,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴DB⊥AC,
∴∠CDB=90°
∵D为AC中点,
∴AB=BC,
在Rt△DEC中,
∵DE=2,tanC=
| 1 |
| 2 |
∴EC=
| DE |
| tanC |
由勾股定理得:DC=2
| 5 |
在Rt△DCB中,BD=DC•tanC=
| 5 |
由勾股定理得:BC=5,
∴AB=BC=5,
∴⊙O的直径为5.
点评:本题主要是作出合适的辅助线.利用了三角形中位线的判定和性质、平行线的性质、切线的判定、直径所对的圆周角等于90°、三角函数值、勾股定理.

练习册系列答案
相关题目
 (2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA=
(2013•东阳市模拟)已知:如图,AB为⊙O的直径,AC、BC为弦,点P为⊙O上一点,弧AC=弧AP,AB=10,tanA= 已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°.
已知:如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,∠BAC=30°. 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为 已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
已知:如图,AB为半圆O的直径,C、D是半圆上的两点,E是AB上除O外的一点,AC与DE交于点F.①
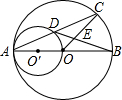 已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.
已知:如图,AB为⊙O的直径,AO为⊙O'的直径,⊙O的弦AC交⊙O'于D点,OC和BD相交于E点,AB=4,∠CAB=30°.求CE、DE的长.