题目内容
如图，四边形BDCE内接于以BC为直径的⊙A，已知：BC=10，cos∠BCD=| 3 |
| 5 |
A、
| ||
B、7
| ||
C、4+3
| ||
D、3+4
|
分析：在Rt△CDB和Rt△CBE中，通过解直角三角形易求得BD、BE的长．
过B作BF⊥DE于F，由圆周角定理知∠BCE=∠BDE，∠BED=∠BCD．
根据这些角的三角函数值以及BD、BE的长，即可求得DF、EF的值，从而得到DE的长．
过B作BF⊥DE于F，由圆周角定理知∠BCE=∠BDE，∠BED=∠BCD．
根据这些角的三角函数值以及BD、BE的长，即可求得DF、EF的值，从而得到DE的长．
解答：
解：过B作BF⊥DE于F．
在Rt△CBD中，BC=10，cos∠BCD=
，
∴BD=8．
在Rt△BCE中，BC=10，∠BCE=30°，
∴BE=5．
在Rt△BDF中，∠BDF=∠BCE=30°，BD=8，
∴DF=BD•cos30°=4
．
在Rt△BEF中，∠BEF=∠BCD，即cos∠BEF=cos∠BCD=
，BE=5，
∴EF=BE•cos∠BEF=3．
∴DE=DF+EF=3+4
，
故选D．
解：过B作BF⊥DE于F．在Rt△CBD中，BC=10，cos∠BCD=
| 3 |
| 5 |
∴BD=8．
在Rt△BCE中，BC=10，∠BCE=30°，
∴BE=5．
在Rt△BDF中，∠BDF=∠BCE=30°，BD=8，
∴DF=BD•cos30°=4
| 3 |
在Rt△BEF中，∠BEF=∠BCD，即cos∠BEF=cos∠BCD=
| 3 |
| 5 |
∴EF=BE•cos∠BEF=3．
∴DE=DF+EF=3+4
| 3 |
故选D．
点评：此题主要考查的是圆周角定理和解直角三角形的综合应用，难度适中．
练习册系列答案
相关题目
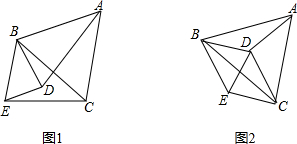意一点，∠ABC=∠DBE，BD=BE．
如图，四边形BDCE内接于以BC为直径的⊙A，已知：
，则线段DE的长是
，则线段DE的长是（ ）
，则线段DE的长是（ ）
