Question

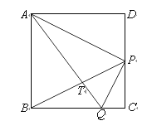
【题目】如图，设ABCD是正方形，P是CD边的中点，点Q在BC边上，且∠APQ=90°，AQ与BP相交于点T，则 的值为多少？

Answer 1

【答案】

【解析】

过B点做BE⊥AQ，垂足为E,PH⊥AQ,垂足为H.设正方形的边长是2,根据三角形ADP与三角形PCQ相似,求出CQ、PQ的长.进而求出BQ、AQ的长.在两个直角三角形中,根据面积公式,分别求出斜边上的高.再求出两个高的比,它就是BT与PT的比.

解:过B点做BE⊥AQ，垂足为E,PH⊥AQ,垂足为H,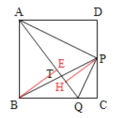

设正方形的边长是2.则DP=CP=1,AD=2，AP=2+1=5,所以AP=.

∠APQ=90,所以∠APD+∠CPQ=90,又∠APD+∠PAD=90,

所以∠PAD=∠CFQ,所以△ADP~ΔPCQ.

所以AD:PC=AP:PQ=DP:CQ.

即2:1=:PQ=1:CQ,

所以PQ=,CQ=.

BQ=2-=.AQ=AB+BQ=2+（）=.

所以AQ=.

=ABBQ=AQBE.

BE=ABBQAQ=2 =.

=APPQ=AQBH,

PH=APPQAQ==1

又BE⊥AQ,PH⊥AQ,

所以ΔBET~ΔPHT,

BT:PT=BE:PH=:1=6:5，

故答案：.