题目内容
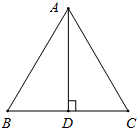如图，等腰△ABC中，AD⊥BC，垂足为D点，且AD=8，△ABC的周长是32，则△ABC的面积________．
48
分析：根据等腰△ABC的性质求得AB+BD=16、在直角三角形ABD中利用勾股定理知AB2-BD2=AD2，据此可以求得BD=6；最后根据三角形的面积公式求△ABC的面积即可．
解答：∵△ABC是等腰三角形，AD⊥BC，
∴BD=CD；
∵等腰△ABC的周长是32，
∴AB+BD+CD+AC=2AB+2BD=32，
∴AB+BD=16 ①，
又由勾股定理知，AB2-BD2=AD2，即16（AB-BD）=64 ②
由①②解得，BD=6；
∴S△ABC=
BC•AD=×12×8=48，即△ABC的面积是48；
故答案是48．
点评：本题考查了勾股定理、等腰三角形的性质．此题根据等腰三角形的“三合一”性质推知点D是边BC上的中点．
分析：根据等腰△ABC的性质求得AB+BD=16、在直角三角形ABD中利用勾股定理知AB2-BD2=AD2，据此可以求得BD=6；最后根据三角形的面积公式求△ABC的面积即可．
解答：∵△ABC是等腰三角形，AD⊥BC，
∴BD=CD；
∵等腰△ABC的周长是32，
∴AB+BD+CD+AC=2AB+2BD=32，
∴AB+BD=16 ①，
又由勾股定理知，AB2-BD2=AD2，即16（AB-BD）=64 ②
由①②解得，BD=6；
∴S△ABC=
BC•AD=×12×8=48，即△ABC的面积是48；故答案是48．
点评：本题考查了勾股定理、等腰三角形的性质．此题根据等腰三角形的“三合一”性质推知点D是边BC上的中点．
练习册系列答案
相关题目
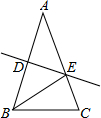如图，等腰△ABC中，AB=AC，∠A=20°．线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于（ ）| A、80° | B、70° | C、60° | D、50° |
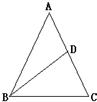13、如图，等腰△ABC中，AB=AC，BD为腰AC的中线，将△ABC分成长12cm和9cm的两段，则等腰△ABC的腰长为
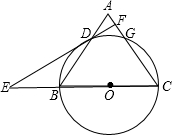如图，等腰△ABC中，AC=BC=10，AB=12，以BC为直径作⊙0交AB于D，交AC于G，DF⊥AC，垂足为F，交CB的延长线于点E，则sinE=
如图，等腰△ABC中，AB=AC，D为BC中点，E为射线AD上一点．
如图，等腰△ABC中，AB=AC，D、E分别为AC、AB的中点．