题目内容
 (2013•临沂)如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是( )
(2013•临沂)如图,在平面直角坐标系中,点A1,A2在x轴上,点B1,B2在y轴上,其坐标分别为A1(1,0),A2(2,0),B1(0,1),B2(0,2),分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是( )分析:根据题意画出树状图,进而得出以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形是等腰三角形的情况,求出概率即可.
解答:解:∵以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,
∴画树状图得:

共可以组成4个三角形,
所作三角形是等腰三角形只有:△OA1B1,△OA2B2,
所作三角形是等腰三角形的概率是:
=
.
故选:D.
∴画树状图得:

共可以组成4个三角形,
所作三角形是等腰三角形只有:△OA1B1,△OA2B2,
所作三角形是等腰三角形的概率是:
| 2 |
| 4 |
| 1 |
| 2 |
故选:D.
点评:此题主要考查了利用树状图求概率以及等腰三角形的判定等知识,利用树状图表示出所有可能是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
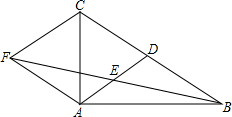 (2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.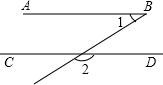 (2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
(2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
 (2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )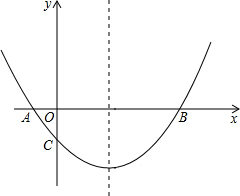 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,