题目内容
(1)方程组 的解是________.
的解是________.
(2)若关于x的方程m(x-1)=2001-n(x-2)有无数个解,则m2003+n2003=________.
解:(1)原方程组可化为 ,
,
①-②×2得,x=0,
代入②得,0+2y=2,
解得y=1,
故原方程组的解为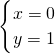 ;
;
故答案为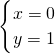 .
.
(2)原方程可化为(m+n)x=2001+2n+m的形式,
因为方程m(x-1)=2001-n(x-2)有无数个解,
所以 ,
,
解得 ,
,
故m2003+n2003=20012003-20012003=0.
故答案为0.
分析:(1)先把方程组中方程x+2(x+2y)=4去括号,合并同类项,再用加减消元法或代入消元法求出x、y的值即可;
(2)先把原方程化为(m+n)x=2001+2n+m的形式,再根据此方程有无数组解得到关于m、n的方程组,求出m、n的值代入代数式m2003+n2003进行计算.
点评:本题考查的是解二元一次方程组,解二元一次方程组的方法有加减消元法和代入消元法,一般选用加减法解二元一次方程组较简单.
 ,
,①-②×2得,x=0,
代入②得,0+2y=2,
解得y=1,
故原方程组的解为
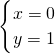 ;
;故答案为
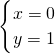 .
.(2)原方程可化为(m+n)x=2001+2n+m的形式,
因为方程m(x-1)=2001-n(x-2)有无数个解,
所以
 ,
,解得
 ,
,故m2003+n2003=20012003-20012003=0.
故答案为0.
分析:(1)先把方程组中方程x+2(x+2y)=4去括号,合并同类项,再用加减消元法或代入消元法求出x、y的值即可;
(2)先把原方程化为(m+n)x=2001+2n+m的形式,再根据此方程有无数组解得到关于m、n的方程组,求出m、n的值代入代数式m2003+n2003进行计算.
点评:本题考查的是解二元一次方程组,解二元一次方程组的方法有加减消元法和代入消元法,一般选用加减法解二元一次方程组较简单.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
方程3x+4y=16与下面哪个方程所组成的方程组的解是
( )
|
A、
| ||
| B、3x-5y=7 | ||
C、
| ||
| D、2(x-y)=3y |
方程2x+3y=11和下列方程构成的方程组的解是
的方程是( )
|
| A、3x+4y=20 |
| B、4x-7y=3 |
| C、2x-7y=1 |
| D、5x-4y=6 |