题目内容
已知,梯形ABCD中,AD∥BC,∠B=45°,∠D=120°,AB=8,求DC的长.
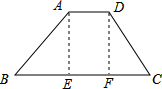 解:如图,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,
解:如图,过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,∴AE∥DF,
∵AD∥BC,
∴四边形AEFD是平行四边形,
∴AE=DF,
∵∠B=45°,AB=8,
∴AE=AB•sin45°=8×
 =4
=4 ,
,∴DF=4
 ,
,∵∠D=120°,
∴∠C=180°-∠ADC=60°,
∴DC=
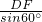 =
=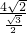 =
= .
.分析:首先根据题意画出图形,然后过点A作AE⊥BC于点E,过点D作DF⊥BC于点F,易得四边形AEFD是平行四边形,则可得AE=DF,然后由三角函数的性质,分别求得AE与DC的长.
点评:此题考查了梯形的性质、平行四边形的判定与性质以及三角函数等知识.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
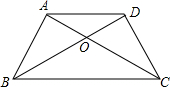 如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.
如图所示,已知等腰梯形ABCD中,AD∥BC,AB=DC,AC与BD相交于点O.请在图中找出一对全等的三角形,并加以证明.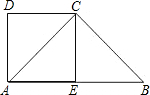 已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC=
已知直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=DC= 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
11、已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( ) 如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )
如图,已知在梯形ABCD中,DC∥AB,AD=BC,∠A=60°,BD平分∠ABC,若AD=1,则对角线BD的长是( )