题目内容
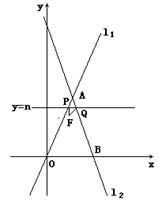
如图,直线 :
: 与直线
与直线 :
: 相交于点
相交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,平行于
,平行于 轴的直线
轴的直线 分别交直线
分别交直线 、直线
、直线 于
于 、
、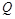 两点(点
两点(点 在
在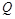 的左侧)
的左侧)
⑴点 的坐标为 ;
的坐标为 ;
⑵如图1,若点 在线段
在线段 上,在
上,在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
⑶如图2.若以点 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角 ,设
,设 与
与 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与 的函数关系式;并注明
的函数关系式;并注明 的取值范围.
的取值范围.
 :
: 与直线
与直线 :
: 相交于点
相交于点 ,直线
,直线 与
与 轴交于点
轴交于点 ,平行于
,平行于 轴的直线
轴的直线 分别交直线
分别交直线 、直线
、直线 于
于 、
、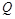 两点(点
两点(点 在
在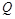 的左侧)
的左侧)⑴点
 的坐标为 ;
的坐标为 ;⑵如图1,若点
 在线段
在线段 上,在
上,在 轴上是否存在一点
轴上是否存在一点 ,使得
,使得 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;⑶如图2.若以点
 为直角顶点,向下作等腰直角
为直角顶点,向下作等腰直角 ,设
,设 与
与 重叠部分的面积为
重叠部分的面积为 ,求
,求 与
与 的函数关系式;并注明
的函数关系式;并注明 的取值范围.
的取值范围.
⑴点 的坐标为(
的坐标为(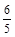 ,
,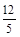 )
)
⑵令 ,则
,则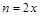 ∴
∴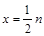
∴点 (
(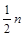 ,
, )
)
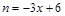 ∴
∴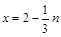
∴点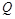 (
(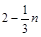 ,
, )
)
∴
作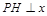 轴于
轴于 当
当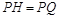 时
时 为等腰直角三角形
为等腰直角三角形
∴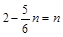
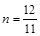
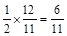 ∴
∴ (
(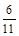 ,0)
,0)
作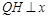 轴于
轴于 当
当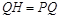 时
时 为等腰直角三角形
为等腰直角三角形
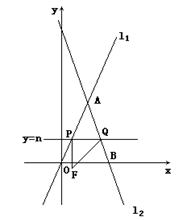
同理可得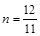
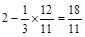 ∴
∴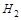 (
(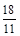 ,0)
,0)
当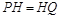 且
且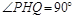 时
时 为等腰直角三角形
为等腰直角三角形
作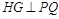 可得
可得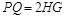
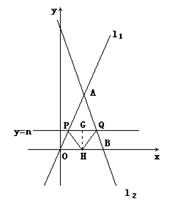
∴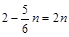
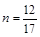
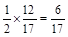
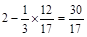
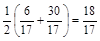 ∴
∴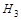 (
(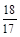 ,0)
,0)
∴ 点的坐标为(
点的坐标为(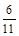 ,0),(
,0),(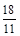 ,0),(
,0),(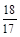 ,0)
,0)
⑶当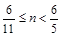 时
时
∴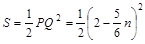
当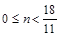 时
时
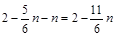
∴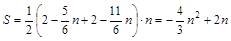
 的坐标为(
的坐标为(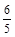 ,
,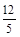 )
)⑵令
 ,则
,则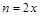 ∴
∴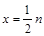
∴点
 (
(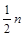 ,
, )
)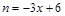 ∴
∴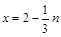
∴点
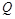 (
(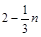 ,
, )
)∴

作
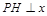 轴于
轴于 当
当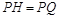 时
时 为等腰直角三角形
为等腰直角三角形
∴
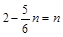
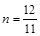
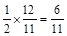 ∴
∴ (
(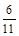 ,0)
,0)作
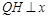 轴于
轴于 当
当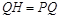 时
时 为等腰直角三角形
为等腰直角三角形
同理可得
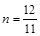
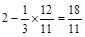 ∴
∴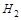 (
(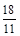 ,0)
,0)当
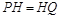 且
且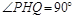 时
时 为等腰直角三角形
为等腰直角三角形作
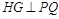 可得
可得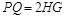

∴
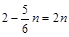
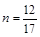
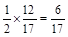
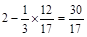
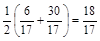 ∴
∴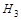 (
(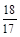 ,0)
,0)∴
 点的坐标为(
点的坐标为(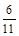 ,0),(
,0),(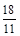 ,0),(
,0),(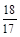 ,0)
,0)⑶当
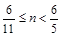 时
时∴
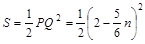
当
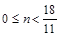 时
时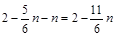
∴
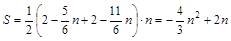
(1)利用两直线相交的性质,使两式相等即可得出答案;
(2)首先表示出PQ的长度,进而得出当PH=HQ且∠PHQ=90°时以及 当PH=PQ时△PQH为等腰直角三角形,分别求出即可;
(3)分别根据当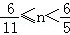 时以及当
时以及当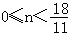 时表示出△PQF与△AOB重叠部分的面积即可.
时表示出△PQF与△AOB重叠部分的面积即可.
(2)首先表示出PQ的长度,进而得出当PH=HQ且∠PHQ=90°时以及 当PH=PQ时△PQH为等腰直角三角形,分别求出即可;
(3)分别根据当
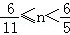 时以及当
时以及当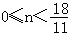 时表示出△PQF与△AOB重叠部分的面积即可.
时表示出△PQF与△AOB重叠部分的面积即可.
练习册系列答案
相关题目
 。
。 的面积。
的面积。
 (2,4)在正比例函数的图象上,这个正比例函数的解析式是 .
(2,4)在正比例函数的图象上,这个正比例函数的解析式是 .

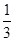 x+b上,则y1,y2,y3的值的大小关系是( ).
x+b上,则y1,y2,y3的值的大小关系是( ).