题目内容
若实数a、b、c满足a+b+c=0,abc=2,c>0,则下列正确的是
- A.ab<0
- B.|a|+|b|≥2
- C.|a|+|b|>4
- D.0<|a|+|b|≤1
B
分析:a+b=-c,ab=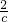 ,则a,b是一元二次方程的两个根,利用其判别式大于等于0即可.
,则a,b是一元二次方程的两个根,利用其判别式大于等于0即可.
解答:∵a+b+c=0,abc=2,
∴a+b=-c,ab=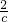 ,
,
∴a,b是一元二次方程cx2+c2x+2=0的两个根,
∴△=c4-8c≥0,
∵c>0,
∴c≥2,
∵|a|+|b|=-a-b
∴|a|+|b|=-a-b=c
∴|a|+|b|≥2,
故选B.
点评:本题考查了根与系数的关系及根的判别式的知识,解题的关键是根据题目的条件得到a、b分别是哪一个方程的两个根.
分析:a+b=-c,ab=
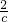 ,则a,b是一元二次方程的两个根,利用其判别式大于等于0即可.
,则a,b是一元二次方程的两个根,利用其判别式大于等于0即可.解答:∵a+b+c=0,abc=2,
∴a+b=-c,ab=
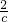 ,
,∴a,b是一元二次方程cx2+c2x+2=0的两个根,
∴△=c4-8c≥0,
∵c>0,
∴c≥2,
∵|a|+|b|=-a-b
∴|a|+|b|=-a-b=c
∴|a|+|b|≥2,
故选B.
点评:本题考查了根与系数的关系及根的判别式的知识,解题的关键是根据题目的条件得到a、b分别是哪一个方程的两个根.

练习册系列答案
相关题目