ƒøƒ⁄»›
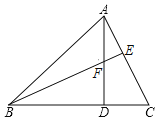
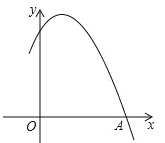
°æƒø°ø»ÁÕº£¨≈◊ŒÔœfly£Ωax2+bx+c”Îx÷·Ωª”⁄A£®©Å1£¨0£©°¢B£®3£¨0£©¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£®0£¨3£©£¨µ„D‘⁄≈◊ŒÔœfl…œ«“∫·◊¯±ÍŒ™2£Æ
£®1£©«Û’‚Ãı≈◊ŒÔœflµƒ±Ì¥Ô Ω£ª
£®2£©Ω´∏√≈◊ŒÔœflœÚœ¬∆Ω“∆£¨ πµ√–¬≈◊ŒÔœflµƒ∂•µ„G‘⁄x÷·…œ£Æ‘≠≈◊ŒÔœfl…œ“ªµ„M∆Ω“∆∫Ûµƒ∂‘”¶µ„Œ™µ„N£¨»Áπ˚°˜AMN «“‘MNŒ™µ◊±flµƒµ»—¸»˝Ω«–Œ£¨«Ûµ„Nµƒ◊¯±Í£ª
£®3£©»Ùµ„PŒ™≈◊ŒÔœfl…œµ⁄“ªœÛœfiƒ⁄µƒ∂ص„£¨π˝µ„B◊˜BE°ÕOP£¨¥π◊„Œ™E£¨µ„QŒ™y÷·…œµƒ“ª∏ˆ∂ص„£¨¡¨Ω”QE°¢QD£¨ ‘«ÛQE+QDµƒ◊Ó–°÷µ£Æ

°æ¥∞∏°ø£®1£©![]() £ª£®2£©µ„
£ª£®2£©µ„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() ªÚ
ªÚ![]() £ª£®3£©
£ª£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©”…≈◊ŒÔœfl”Îx÷·¡ΩΩªµ„…ËΩªµ„ Ω£¨∞—µ„C¥˙»Îº¥«Ûµ√≈◊ŒÔœfl±Ì¥Ô Ω£ª
£®2£©”…‘≠≈◊ŒÔœfl∂•µ„ Ωø…÷™£¨œÚœ¬∆Ω“∆4∏ˆµ•Œª∫Û∂•µ„¬‰‘⁄x÷·…œ£¨π MN£Ω4«“MN°Õx÷·£Æ”…”⁄°˜AMNŒ™µ»—¸»˝Ω«–Œ«“MNŒ™µ◊±fl£¨π ”–x÷·¥π÷±∆Ω∑÷MN£¨µ√µΩµ„N◊›◊¯±ÍŒ™©Å2£¨¥˙»Î–¬≈◊ŒÔœflΩ‚Œˆ ΩΩ‚∑Ω≥ú¥«Ûµ√µ„N∫·◊¯±Í£Æ
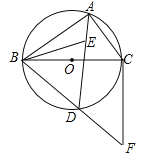
£®3£©◊˜µ„Dπÿ”⁄y÷·µƒ∂‘≥∆µ„D'£¨∏˘æ›÷·∂‘≥∆–‘÷ º¥”–QD£ΩQD'£¨“◊µ√µ±µ„D'°¢Q°¢E‘⁄Õ¨“ª÷±œfl…œ ±£¨QE+QD£ΩQE+QD'£ΩED'◊Ó–°£Æ”…”⁄µ„EÀʵ„P‘À∂Ø“≤ «“ª∏ˆ∂ص„£¨”…°œOEB£Ω90°„«“O°¢B «∂®µ„ø…µ√µ„Eµƒ‘À∂ØπϺ£Œ™‘≤ª°£Æπ µ±µ„E‘À∂ØµΩµ„D'”Α≤–ƒÀ˘¡¨œfl∂Œ…œ ±£¨D'E◊Ó–°£Æ«Û≥ˆ‘≤–ƒFµƒ◊¯±Í£¨º¥«Û≥ˆD'F∫Õ∞Îæ∂r£¨À˘“‘D'E£ΩD'F©År£¨À˘«Ûº¥Œ™QE+QDµƒ◊Ó–°÷µ£Æ
Ω‚£∫£®1£©≈◊ŒÔœfl”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() £¨
£¨
…ËΩªµ„ ΩŒ™![]() £¨
£¨
![]() ≈◊ŒÔœflæ≠π˝µ„
≈◊ŒÔœflæ≠π˝µ„![]() £¨
£¨
![]()
Ω‚µ√£∫![]() £¨
£¨
![]() ≈◊ŒÔœfl±Ì¥Ô ΩŒ™
≈◊ŒÔœfl±Ì¥Ô ΩŒ™![]()
£®2£©![]()
![]() œÚœ¬∆Ω“∆∫Û–¬≈◊ŒÔœflŒ™
œÚœ¬∆Ω“∆∫Û–¬≈◊ŒÔœflŒ™![]() £¨∂•µ„
£¨∂•µ„![]() £¨º¥≈◊ŒÔœflœÚœ¬∆Ω“∆4∏ˆµ•Œª
£¨º¥≈◊ŒÔœflœÚœ¬∆Ω“∆4∏ˆµ•Œª
![]() ‘≠≈◊ŒÔœfl…œ“ªµ„
‘≠≈◊ŒÔœfl…œ“ªµ„![]() ∆Ω“∆∫Ûµƒ∂‘”¶µ„Œ™µ„N£¨
∆Ω“∆∫Ûµƒ∂‘”¶µ„Œ™µ„N£¨
![]() £¨
£¨![]() ÷·
÷·
![]() «“‘
«“‘![]() Œ™µ◊±flµƒµ»—¸»˝Ω«–Œ£¨«“µ„
Œ™µ◊±flµƒµ»—¸»˝Ω«–Œ£¨«“µ„![]() ‘⁄
‘⁄![]() ÷·…œ
÷·…œ
![]() ÷·¥π÷±∆Ω∑÷
÷·¥π÷±∆Ω∑÷![]() £¨
£¨
![]() µƒ◊›◊¯±ÍŒ™
µƒ◊›◊¯±ÍŒ™![]()
![]() ‘⁄–¬≈◊ŒÔœflŒ™
‘⁄–¬≈◊ŒÔœflŒ™![]() …œ£¨
…œ£¨
![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]()
![]() µ„
µ„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() ªÚ
ªÚ![]() £Æ
£Æ
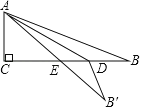
£®3£©»Áœ¬ÕºÀ˘ 棨◊˜µ„![]() πÿ”⁄
πÿ”⁄![]() ÷·µƒ∂‘≥∆µ„µ„
÷·µƒ∂‘≥∆µ„µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨»°
£¨»°![]() ÷–µ„
÷–µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨
![]() µ„D‘⁄≈◊ŒÔœfl…œ«“∫·◊¯±ÍŒ™2£¨µ„
µ„D‘⁄≈◊ŒÔœfl…œ«“∫·◊¯±ÍŒ™2£¨µ„![]() Œ™
Œ™![]() ÷·…œµƒ∂ص„£¨
÷·…œµƒ∂ص„£¨
![]() £¨
£¨![]() £¨
£¨
![]() µ±µ„
µ±µ„![]() °¢
°¢![]() °¢
°¢![]() ‘⁄Õ¨“ª÷±œfl…œ ±£¨
‘⁄Õ¨“ª÷±œfl…œ ±£¨![]() ◊Ó–°£¨
◊Ó–°£¨
![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() Œ™≈◊ŒÔœfl…œµ⁄“ªœÛœfiƒ⁄µƒ∂ص„£¨
Œ™≈◊ŒÔœfl…œµ⁄“ªœÛœfiƒ⁄µƒ∂ص„£¨
![]()
![]() µ„
µ„![]() ‘⁄“‘
‘⁄“‘![]() Œ™÷±æ∂µƒ‘≤‘⁄µ⁄“ªœÛœfiƒ⁄µƒª°…œ‘À∂Ø£¨
Œ™÷±æ∂µƒ‘≤‘⁄µ⁄“ªœÛœfiƒ⁄µƒª°…œ‘À∂Ø£¨
![]() ‘≤–ƒ
‘≤–ƒ![]() £¨
£¨![]() £¨
£¨
![]() µ±µ„
µ±µ„![]() ‘⁄œfl∂Œ
‘⁄œfl∂Œ![]() …œ ±£¨
…œ ±£¨![]() ◊Ó–°£¨
◊Ó–°£¨
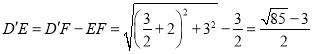
![]() µƒ◊Ó–°÷µŒ™
µƒ◊Ó–°÷µŒ™![]() £Æ
£Æ

°æƒø°øπ‚√˜÷–—ß»´Ã—߅˙900»À≤Œº”…Áª· µº˘ªÓ∂Ø£¨¥”÷–Àʪ˙≥È»°50»Àµƒ…Áª· µº˘ªÓ∂Ø≥…º®÷∆≥…»ÁÕºÀ˘ 浃Ãı–ŒÕ≥º∆Õº£¨Ω·∫œÕº÷–À˘∏¯–≈œ¢Ω‚¥œ¬¡–Œ £∫
![]() ÃÓ–¥œ¬±Ì£∫
ÃÓ–¥œ¬±Ì£∫
÷–Œª ˝ | ÷⁄ ˝ | |
Àʪ˙≥È»°µƒ50»Àµƒ…Áª· µº˘ªÓ∂Ø≥…º® |
![]() π¿º∆π‚√˜÷–—ß»´Ã—߅˙…Áª· µº˘ªÓ∂Ø≥…º®µƒ◊‹∑÷£Æ
π¿º∆π‚√˜÷–—ß»´Ã—߅˙…Áª· µº˘ªÓ∂Ø≥…º®µƒ◊‹∑÷£Æ