Question

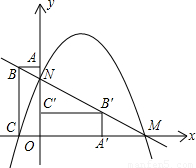
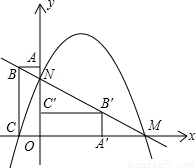
（2008•吉林）如图，在平面直角坐标系中，矩形OABC的顶点A（0，3），C（-1，0），将矩形OABC绕原点O顺时针方向旋转90度，得矩形OA′B′C′矩形设直线BB’与x轴交于点M，与y轴交于点N，抛物线经过点C，M，N点．
解答下列问题：
（1）设直线BB′表示的函数解析式为y=mx+n，求m，n；
（2）求抛物线表示的二次函数的解析式；
（3）在抛物线上求出使S_△PB‘C‘=S_矩形OABC的所有点P的坐标．

Answer 1

【答案】分析：（1）已知A（0，3），C（-1，0），就可以得到OA=3，OC=1，就可以得到B、B′的坐标，根据待定系数法就可以求出直线BB′，的解析式；得到m、n的值．
（2）已知直线BB′的解析式，可以求得与x轴，y轴的交点M、N的坐标，根据待定系数法就可以求出二次函数的解析式．
（3）矩形OABC的面积容易求得，△PB'C'的底边B'C'的边长可以得到，B'C'边上的高线长就是P点的纵坐标-1的绝对值．设P的纵坐标是y，根据三角形的面积就可以得到一个关于y的方程，就可以解得y的值．进而就可以求出P的坐标．
解答：解：（1）∵四边形OABC是矩形，
∴B（-1，3）（1分）
根据题意，得B′（3，1）
把B（-1，3），B′（3，1）代入y=mx+n中，（1分）
解得
∴m=-，n=

（2）由（1）得y=-x+，
∴N（0，），M（5，0）（2分）
设二次函数解析式为y=ax²+bx+c，
把C（-1，0），N（0，），M（5，0）代入得：，
解得（1分）
∴二次函数的解析式为y=-x²+2x+（1分）

（3）∵S_矩形OABC=3×1=3
∴S_△PB‘C’=3
又∵由（1）（2）知B'C'=BC=3，
∴点P到B'C'的距离为2，则P点的纵坐标为3或-1
当y=3时，3=-x²+2x+，即x²-4x+1=0
解得x=2±
∴P₁（2+，3），P₂（2-，3），（2分）
当y=-1时，-1=-x²+2x+，即x²-4x-7=0
解得x=2±
∴P₃（2+，-1），P₄（2-，-1）（2分）
∴P点坐标（2+，3），（2-，3），（2+，-1），（2-，-1）．
点评：本题主要考查了待定系数法求函数的解析式，注意数形结合是解决本题的关键．