题目内容
已知a,b,c是全不相等的正实数,求证:
+
+
>3.
【证明】方法一:要证++>3,
只需证明
+
-1+
+
-1+
+
-1>3,
即证:+++++>6.
由a,b,c为全不相等的正实数得
+>2,+>2,+>2,
∴+++++>6,
∴++>3成立.
方法二:∵a,b,c全不相等,
∴与,与,与全不相等,
∴+>2,+>2,+>2,
三式相加得+++++>6,
∴(+-1)+(+
-1)+(+-1)>3,
即++>3.
练习册系列答案
口算题天天练系列答案
相关题目
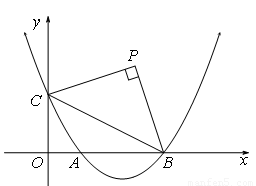
（b是实数且b>2）与x轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C．
（b是实数且b＞2）与x轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C.