题目内容
 (2012•黄石)如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=
(2012•黄石)如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=4
-1
| 3 |
4
-1
.| 3 |
分析:先根据已知条件,求出经过t秒后,OC的长,当⊙P与OA,即与x轴相切时,如图所示,则切点为O,此时PC=OP,过P作PE⊥OC,利用垂径定理和解直角三角形的有关知识即可求出t的值.
解答:解:∵已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,
∴经过t秒后,
∴OA=1+t,
∵四边形OABC是菱形,
∴OC=1+t,
当⊙P与OA,即与x轴相切时,如图所示,则切点为O,此时PC=OP,过P作PE⊥OC,
∴OE=CE=
OC,
∴OE=
,
在Rt△OPE中,
OE=OP•cos30°=2
,
∴
=2
,
∴t=4
-1,
故答案为:4
-1.
∴经过t秒后,
∴OA=1+t,
∵四边形OABC是菱形,
∴OC=1+t,
当⊙P与OA,即与x轴相切时,如图所示,则切点为O,此时PC=OP,过P作PE⊥OC,

∴OE=CE=
| 1 |
| 2 |
∴OE=
| 1+t |
| 2 |
在Rt△OPE中,
OE=OP•cos30°=2
| 3 |
∴
| 1+t |
| 2 |
| 3 |
∴t=4
| 3 |
故答案为:4
| 3 |
点评:本题综合性的考查了菱形的性质、坐标与图形性质、切线的性质、垂径定理的运用以及解直角三角形的有关知识,属于中档题目.

练习册系列答案
相关题目
 已确定支架AB高为25cm,求支架CD的高(结果精确到1cm)?
已确定支架AB高为25cm,求支架CD的高(结果精确到1cm)? (2012•黄石)如图所示,已知A(
(2012•黄石)如图所示,已知A(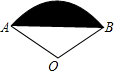 (2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( )
(2012•黄石)如图所示,扇形AOB的圆心角为120°,半径为2,则图中阴影部分的面积为( ) (2012•黄石)如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为( )
(2012•黄石)如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则AF长为( )