题目内容
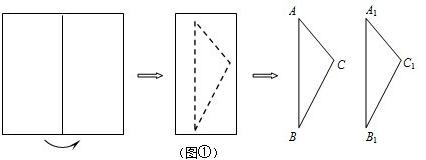
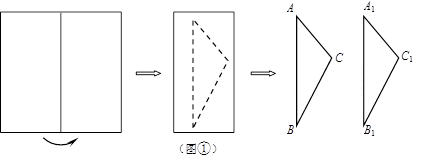
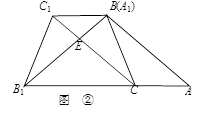
将一张矩形纸片ABCD如图那样折叠，使顶点C落在C'处，若AB=3，∠C′ED=30°，则折痕DE的长为________．
6
分析：先由矩形的性质得到AB=DC=3，∠C=90°，再根据折叠的性质得到∠DEC=∠DEC′=30°，然后根据含30度的直角三角形三边的关系得到DE=2DC=6．
解答：∵四边形ABCD为矩形，
∴AB=DC=3，∠C=90°，
∵矩形纸片ABCD沿DE折叠，使顶点C落在C'处，
∴∠DEC=∠DEC′=30°，
∴DE=2DC=6．
故答案为6．
点评：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了含30度的直角三角形三边的关系以及矩形的性质．
分析：先由矩形的性质得到AB=DC=3，∠C=90°，再根据折叠的性质得到∠DEC=∠DEC′=30°，然后根据含30度的直角三角形三边的关系得到DE=2DC=6．
解答：∵四边形ABCD为矩形，
∴AB=DC=3，∠C=90°，
∵矩形纸片ABCD沿DE折叠，使顶点C落在C'处，
∴∠DEC=∠DEC′=30°，
∴DE=2DC=6．
故答案为6．
点评：本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了含30度的直角三角形三边的关系以及矩形的性质．
练习册系列答案
相关题目
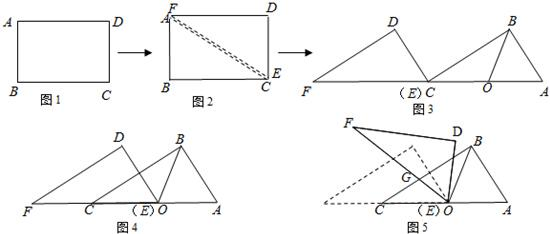
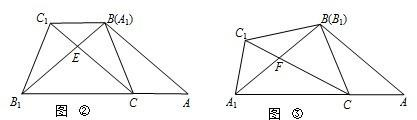
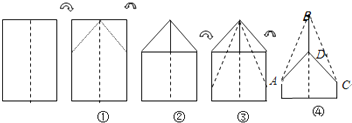
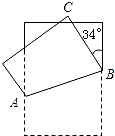将一张矩形纸片折叠成如图所示的形状，则∠ABC=
