Question

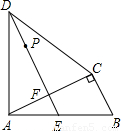
如图，四边形ABCD中，AD=CD，∠DAB=∠ACB=90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．已知AB=15cm，BC=9cm，P是射线DE上的动点．设DP=xcm（x＞0），四边形BCDP的面积为ycm²．
（1）求y关于x的函数关系式；
（2）当x为何值时，△PBC的周长最小，并求出此时y的值．

Answer 1

【答案】分析：（1）根据DE⊥AC得到∠DFC=∠FCB=90°，从而得到四边形BCDP是梯形，然后在Rt△ABC中利用AC²+BC²=AB²求得AC，从而得到CF=AF=6，然后表示出y与x之间的函数关系即可；
（2）根据BC=9（定值），得到要使△PBC的周长最小，只需PB+PC最小，根据点P是线段AC垂直平分线上的点得到PA=PC，从而得到PB+PC=PB+PA，故只要求PB+PA最小．然后分△DAE∽△ACB和△AFE∽△ACB即可求得AE的长．
解答：解：（1）∵DE⊥AC，
∴∠DFC=∠FCB=90°．
∴BC∥DF，
∴四边形BCDP是梯形．
在Rt△ABC中，AC²+BC²=AB²，
∴．
在△ACD中，∵DA=DC，DF⊥AC，
∴CF=AF=6，
∴（x＞0）．

（2）∵BC=9（定值）．理由如下：
∴要使△PBC的周长最小，只需PB+PC最小．
∵点P是线段AC垂直平分线上的点，
∴PA=PC，
∴PB+PC=PB+PA，故只要求PB+PA最小．
如图，显然当P与E重合时PB+PA最小，
此时x=DP=DE，PB+PA=AB，
在△DAE和△ABC中，
∵BC∥DF，
∴∠AEF=∠B，
∵∠DFA=∠ACB=90°，
∴△DAE∽△ACB，
∴，
即，
在△AFE和△ACB中
∵∠FAE=∠CAB，∠AFE=∠ACB=90°，
∴△AFE∽△ACB，
∴，
即，
∴AE=．
在Rt△ADE和△CAB中
∵∠AEF=∠B，
∴tan∠AEF=tan∠B，
∴即，
∴AD=10，
∴．
∴当时，△PBC的周长最小，此时．
点评：本题考查了等腰三角形的性质，相似三角形的性质和判定，勾股定理的应用，通过做此题培养了学生的推理能力和计算能力，题型比较好，综合性也比较强．