Question

已知：如图，CE是Rt△ABC的斜边AB上的高，BG⊥AP．求证：CE²=ED•EP．

Answer 1

证明：∵CE是Rt△ABC的斜边AB上的高，
∴△ACE∽△CBE，
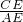∴=，即CE²=AE•BE．
∵CE是Rt△ABC的斜边AB上的高，BG⊥AP，
∴∠P+∠PAE=90°，∠DBE+∠PAE=90°，
∴∠P=∠DBE，
又∵∠AEP=∠DEB=90°，
∴△AEP∽△DEB；
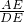∴=，即AE•BE=ED•EP，
又∵CE²=AE•BE，
∴CE²=ED•EP．
分析：通过相似三角形△ACE∽△CBE的对应边成比例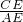知=即CE²=AE•BE；由相似三角形△AEP∽△DEB的对应边成比例知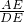=，即AE•BE=ED•EP；最后根据等量代换即可证得结论．
点评：此题综合运用了相似三角形的判定和性质．注意：直角三角形被斜边上的高分成的两个三角形和原三角形相似．