题目内容
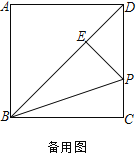
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.
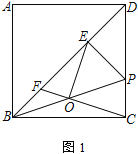
(1)O为BP的中点,连接CO并延长交BD于点F
①如图1,连接OE,求证:OE⊥OC;
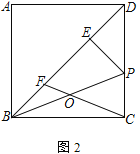
②如图2,若![]() ,求DP的长;
,求DP的长;
(2)![]() =___________
=___________
【答案】(1)①证明见解析;②DP=4;(2)![]()
【解析】
(1) ①首先得出∠POE=2∠DBP,∠POC=2∠CBP,从而得到∠COE=∠POE+∠POC=2(∠DBP+∠CBP)=90°,即可得到结论;②连接OE、CE,把△DEC绕点C逆时针旋转90°得到△BGC,连结FG,则△BGC≌△DEC,得到EC=GC,DE=BG,∠GCB=∠ECD,∠GBC=∠EDC=45°,进而得到∠GCF=∠ECF.再证△GCF≌△ECF,得到EF=FG,在Rt△FBG中,有BF+BG=FG,即BF+DE=EF,由已知![]() ,设BF=3x,EF=5x,则DE=4x,得到3x+4x+5x=6
,设BF=3x,EF=5x,则DE=4x,得到3x+4x+5x=6![]() ,解得x的值,进而得到结论.;(2)由正方形的性质和PE⊥BD得到DP=
,解得x的值,进而得到结论.;(2)由正方形的性质和PE⊥BD得到DP=![]() EP,即EP=
EP,即EP=![]() DP,代入原式即可得到结论.
DP,代入原式即可得到结论.
(1) ① ∵∠PEB=∠PCB=90°,O为BP的中点
∴OE=OB=OP=OC
∴∠POE=2∠DBP,∠POC=2∠CBP
∴∠COE=∠POE+∠POC=2(∠DBP+∠CBP)=90°
∴OE⊥OC
② 连接OE、CE

∵△COE为等腰直角三角形
∴∠ECF=45°
在等腰Rt△BCD中,BF2+DE2=EF2
设BF=3x,EF=5x,则DE=4x
∴3x+4x+5x=![]() ,解得x=
,解得x=![]()
∴DP=![]() DE=
DE=![]()
(2) ∵![]()
∴![]() .
.

练习册系列答案
相关题目