题目内容
 如图,S△ABC=60,BE:CE=1:2,AD:CD=3:1,则S四边形DOEC=
如图,S△ABC=60,BE:CE=1:2,AD:CD=3:1,则S四边形DOEC=
- A.10
- B.11
- C.12
- D.13
A
分析:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.根据图形和三角形的面积公式列出关于a、b、x、y的四元一次方程组,通过解方程组即可求得四边形CDOE的面积.
解答: 解:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.
解:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.
∵S△ABC=60,BE:CE=1:2,AD:CD=3:1,
∴ ,
,
解得, ,
,
所以四边形DOEC的面积是10.
故选A.
点评:本题考查了三角形的面积.解得该题的关键是找出同高的三角形的面积间的数量关系.
分析:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.根据图形和三角形的面积公式列出关于a、b、x、y的四元一次方程组,通过解方程组即可求得四边形CDOE的面积.
解答:
 解:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.
解:设S△ADO=x,S四边形DOEC=y,S△ABO=a,S△BOE=b.∵S△ABC=60,BE:CE=1:2,AD:CD=3:1,
∴
 ,
,解得,
 ,
,所以四边形DOEC的面积是10.
故选A.
点评:本题考查了三角形的面积.解得该题的关键是找出同高的三角形的面积间的数量关系.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
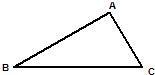

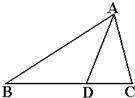 20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线,
20、如图,在△ABC中,∠B=42°,∠C=72°,AD是△ABC的角平分线, 8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
8、如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )