Question

在平面直角坐标系中有两点A（-1，2），B（3，2），C是坐标轴上的一点，若△ABC是直角三角形，则满足条件的点C有

1. A.
   3个
2. B.
   4个
3. C.
   5个
4. D.
   6个

Answer 1

C
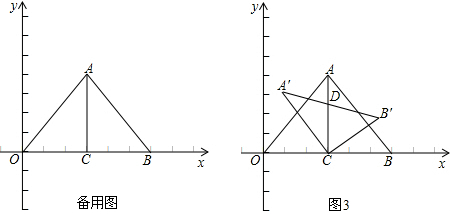
分析：因为A，B的纵坐标相等，所以AB∥x轴．因为C是坐标轴上的一点，所以过点A向x轴引垂线，过点B向x轴引垂线，分别可得一点，根据直径所对的圆周角为直角，以AB为直径做圆，根据A和B的坐标求出AB的长度，即为圆的直径，可得出半径的长，进而判断得出圆与x轴相切，可得出圆与坐标轴交于3点．所以满足条件的点共有5个．
解答：根据题意画出相应的图形，如图所示：

分三种情况考虑：当A为直角顶点时，过A作AC⊥x轴，连接BC，此时满足题意的点为C₁；
当B为直角顶点时，过B作BC⊥x轴，连接AC，此时满足题意的点为C₂；
当C为直角顶点时，以AB为直径作圆，由A（-1，2），B（3，2），得到AB=4，可得此圆与x轴相切，
∴此圆与坐标轴有三个交点，分别为C₃，C₄，C₅，
如图所示，根据直径所对的圆周角为直角可得此3点满足题意，
综上，所有满足题意的C有5个．
故选C．
点评：此题考查了圆周角定理，勾股定理，以及坐标与图形性质，利用了分类讨论及数形结合的思想，学生做题时注意要全面，不要遗漏解的个数．