题目内容
如图，点I是三角形ABC的内心，连接AI并延长交BC于点E，交三角形ABC的外接圆于点D，连接BD．求证．BD2=DE•DA．
解：∵点I是三角形ABC的内心，
∴∠DAC=∠DAB．
又∵∠DAC=∠DBC，
∴∠DBC=∠DAB．
而∠D公共，
∴△DBE∽△DAB．
∴BD2=DE•DA．
分析：由同弧所对的圆周角相等及内心的定义可得∠DBC=∠DAB，从而得到△DBE∽△DAB，写出相似比即可．
点评：记住同弧或等弧所对的圆周角相等，理解内心的定义．熟练掌握三角形相似的判定定理和性质．
∴∠DAC=∠DAB．
又∵∠DAC=∠DBC，
∴∠DBC=∠DAB．
而∠D公共，
∴△DBE∽△DAB．
∴BD2=DE•DA．
分析：由同弧所对的圆周角相等及内心的定义可得∠DBC=∠DAB，从而得到△DBE∽△DAB，写出相似比即可．
点评：记住同弧或等弧所对的圆周角相等，理解内心的定义．熟练掌握三角形相似的判定定理和性质．
练习册系列答案
相关题目
18、如图，点I是三角形ABC的内心，连接AI并延长交BC于点E，交三角形ABC的外接圆于点D，连接BD．求证．BD2=DE•DA．
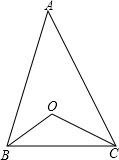如图，点O是三角形两条角平分线的交点，若∠BOC=110°，则∠A=
如图，点O是三角形两条角平分线的交点，若∠BOC=110°，则∠A=________．