题目内容
平行四边形ABCD的两条对角线AC、BD相交于O，AB=
，AO=2，BO=1，则平行四边形ABCD同时也是________形．
菱
分析：利用勾股定理的逆定理可得出：对角线互相垂直，进而判定出平行四边形ABCD同时也是菱形．
解答：
∵AB=，AO=2，BO=1，
∴AB2=5，AO2=4，B02=1，
∴AB2=AO2+B02，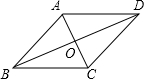
∴三角形AOB是直角三角形，
∴AO⊥BO，
即AC⊥BD，
∵四边形ABCD为平行四边形，
∴四边形ABCD为菱形，
故答案为：菱．
点评：本题考查了勾股定理的逆定理和菱形的判定方法，菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等；③对角线互相垂直平分的四边形是菱形．
分析：利用勾股定理的逆定理可得出：对角线互相垂直，进而判定出平行四边形ABCD同时也是菱形．
解答：
∵AB=
，AO=2，BO=1，∴AB2=5，AO2=4，B02=1，
∴AB2=AO2+B02，
∴三角形AOB是直角三角形，
∴AO⊥BO，
即AC⊥BD，
∵四边形ABCD为平行四边形，
∴四边形ABCD为菱形，
故答案为：菱．
点评：本题考查了勾股定理的逆定理和菱形的判定方法，菱形的判定方法有三种：①定义：一组邻边相等的平行四边形是菱形；②四边相等；③对角线互相垂直平分的四边形是菱形．
练习册系列答案
相关题目
（2012•永州）如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E．若△CDE的周长为10，则平行四边形ABCD的周长为
如图，E、F是平行四边形ABCD的对角线AC上的点，AE=CF．求证：BE=DF．
如图，点E在平行四边形ABCD的对角线BD上．