题目内容
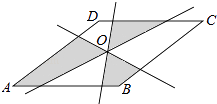
【题目】如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N两点.若AM=2,则线段ON的长为( ) 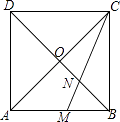
A.![]()
B.![]()
C.1
D.![]()
【答案】C
【解析】解:作MH⊥AC于H,如图, 
∵四边形ABCD为正方形,
∴∠MAH=45°,
∴△AMH为等腰直角三角形,
∴AH=MH= ![]() AM=
AM= ![]() ×2=
×2= ![]() ,
,
∵CM平分∠ACB,
∴BM=MH= ![]() ,
,
∴AB=2+ ![]() ,
,
∴AC= ![]() AB=
AB= ![]() (2+
(2+ ![]() )=2
)=2 ![]() +2,
+2,
∴OC= ![]() AC=
AC= ![]() +1,CH=AC﹣AH=2
+1,CH=AC﹣AH=2 ![]() +2﹣
+2﹣ ![]() =2+
=2+ ![]() ,
,
∵BD⊥AC,
∴ON∥MH,
∴△CON∽△CHM,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴ON=1.
故选C.
【考点精析】关于本题考查的角平分线的性质定理和正方形的性质,需要了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.

练习册系列答案
相关题目