题目内容
19．若双曲线y=$\frac{k}{x}$与直线y=2x+1一个交点的横坐标为-1，则k的值为1．分析 将x=-1代入直线y=2x+1，求出该点纵坐标，从而得到此交点的坐标，将该交点坐标代入y=$\frac{k}{x}$即可求出k的值．
解答 解：将x=-1代入直线y=2x+1得，y=-2+1=-1，
则交点坐标为（-1，-1），
将（-1，-1）代入y=$\frac{k}{x}$得，
k=-1×（-1）=1，
故答案为1．
点评 本题考查了反比例函数与一次函数的交点问题，知道交点坐标符合两函数解析式是解题的关键．
练习册系列答案
相关题目
20．
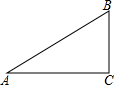如图在Rt△ABC中，∠C=90°，AB=15，sinA=$\frac{1}{3}$，则BC等于（ ）
如图在Rt△ABC中，∠C=90°，AB=15，sinA=$\frac{1}{3}$，则BC等于（ ）| A． | 45 | B． | 5 | C． | $\frac{1}{5}$ | D． | $\frac{1}{45}$ |
7．已知抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点，与y轴交于C点，其中A（-1，0）点D是抛物线y=$\frac{1}{2}$x2+bx-2的顶点，点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，m的值是（ ）
| A． | $\frac{25}{40}$ | B． | $\frac{24}{41}$ | C． | $\frac{23}{40}$ | D． | $\frac{25}{41}$ |
14．已知：AB⊥CD，垂足为O，EF经过点O，∠AOE=35°，则∠DOF等于（ ）
| A． | 65° | B． | 55°或125° | C． | 35° | D． | 65°或155° |
4．
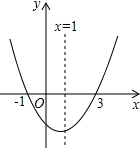已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0；②b+2a=0；③x=3是关于x的方程ax2+bx+c=0（a≠0）的一个根；④a+c＞b；⑤3a+c=0．其中正确的结论有（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0；②b+2a=0；③x=3是关于x的方程ax2+bx+c=0（a≠0）的一个根；④a+c＞b；⑤3a+c=0．其中正确的结论有（ ）| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |
11．
如图，同心圆O中，大圆半径OA、OB分别交小圆于D、C，OA⊥OB，若四边形ABCD的面积为50，则图中阴影部分的面积为（ ）
如图，同心圆O中，大圆半径OA、OB分别交小圆于D、C，OA⊥OB，若四边形ABCD的面积为50，则图中阴影部分的面积为（ ）| A． | 75 | B． | 50π | C． | 75π | D． | 75$\sqrt{2}$ |
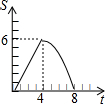
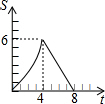
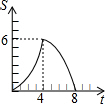
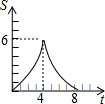
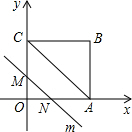在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M，N，直线m运动的时间为t（秒）．设△OMN的面积为S，那么能反映S与t之间函数关系的大致图象是（ ）
