题目内容
已知正方形ABCD的边长为6cm,点E是射线BC上的一个动点,连接AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在 点B′处.
点B′处.
(1)当 =1时,CF=______cm,
=1时,CF=______cm,
(2)当 =2时,求sin∠DAB′的值;
=2时,求sin∠DAB′的值;
(3)当 =x时(点C与点E不重合),请写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,(只要写出结论,不要解题过程).
=x时(点C与点E不重合),请写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,(只要写出结论,不要解题过程).
解:(1)当 =1时,∵AB∥DF,
=1时,∵AB∥DF,
∴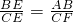 =1.
=1.
∵AB=6,
∴CF=6cm.
(2)①如图1.当点E在BC上时,延长AB′交DC于点M.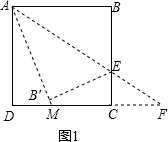
∵AB∥CF,
∴△ABE∽△FCE,
∴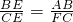 .
.
∵ =2,
=2,
∴CF=3;
∵AB∥CF,
∴∠BAE=∠F;
又∠BAE=∠B′AE,
∴∠B′AE=∠F,
∴MA=MF.
令MA=MF=k,则MC=k-3,DM=9-k.
在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,
解得k=MA= ,
,
∴DM= .
.
∴sin∠DAB′=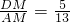 .
.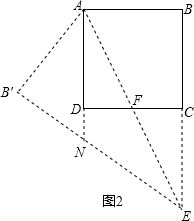
②如图2.当点E在BC延长线上时,延长AD交B′E于点N,同①可得NA=NE.
设NA=NE=m,则B′N=12-m,
在Rt△AB′N中,由勾股定理,得m2=(12-m)2+62,
解得m=AN= ,
,
∴B′N= ,
,
∴sin∠DAB′=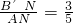 .
.
(3)当 =x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.分两种情况:
=x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.分两种情况:
①当点E在BC上时.
∵ =x,
=x,
∴ =
= ,BE=
,BE=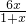 ,
,
∴y= ×AB×BE,即y=
×AB×BE,即y=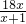 .
.
②当点E在BC延长线上时,△ADF的面积为所求.
∵ =x,∴
=x,∴ =
= ,
,
又∵AD=6,
∴FC= ,DF=6-
,DF=6- ;
;
∴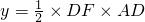 ,
,
∴y=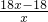 .
.
分析:(1)当 =1时,由AB∥DF,得
=1时,由AB∥DF,得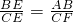 ,由AB=6,CF可求.
,由AB=6,CF可求.
(2)当 =2时,①点E在线段AB上时,延长AB′交DC于点M,求sin∠DAB′的值,即求
=2时,①点E在线段AB上时,延长AB′交DC于点M,求sin∠DAB′的值,即求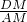 的值,由AB∥CF,可得△ABE∽△FCE,即得
的值,由AB∥CF,可得△ABE∽△FCE,即得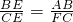 =2,又AB=6,可得CF=3;由∠BAE=∠F,又∠BAE=∠B′AE,可得∠B′AE=∠F,即MA=MF.设MA=MF=k,则MC=k-3,DM=9-k.在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,解得k=
=2,又AB=6,可得CF=3;由∠BAE=∠F,又∠BAE=∠B′AE,可得∠B′AE=∠F,即MA=MF.设MA=MF=k,则MC=k-3,DM=9-k.在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,解得k= .得DM=
.得DM= ,
,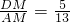 .即sin∠DAB′的值可求.②点E在不在线段AB上时,如图2所示,求sin∠DAB′的值,即是求
.即sin∠DAB′的值可求.②点E在不在线段AB上时,如图2所示,求sin∠DAB′的值,即是求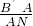 的值,同理可求.
的值,同理可求.
(3)当 =x时,求△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,同理需分两种情况,①动点的位置在线段BC上,所求△AB′E的面积即为△ABE的面积;②动点的位置不在线段BC上,△ADF的面积为所求.
=x时,求△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,同理需分两种情况,①动点的位置在线段BC上,所求△AB′E的面积即为△ABE的面积;②动点的位置不在线段BC上,△ADF的面积为所求.
点评:此题综合考查函数、正方形,平行线分线段成比例定理、图形的旋转、等知识点.分类讨论的思想,综合性强.
 =1时,∵AB∥DF,
=1时,∵AB∥DF,∴
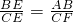 =1.
=1.∵AB=6,
∴CF=6cm.
(2)①如图1.当点E在BC上时,延长AB′交DC于点M.

∵AB∥CF,
∴△ABE∽△FCE,
∴
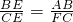 .
.∵
 =2,
=2,∴CF=3;
∵AB∥CF,
∴∠BAE=∠F;
又∠BAE=∠B′AE,
∴∠B′AE=∠F,
∴MA=MF.
令MA=MF=k,则MC=k-3,DM=9-k.
在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,
解得k=MA=
 ,
,∴DM=
 .
.∴sin∠DAB′=
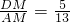 .
.
②如图2.当点E在BC延长线上时,延长AD交B′E于点N,同①可得NA=NE.
设NA=NE=m,则B′N=12-m,
在Rt△AB′N中,由勾股定理,得m2=(12-m)2+62,
解得m=AN=
 ,
,∴B′N=
 ,
,∴sin∠DAB′=
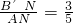 .
.(3)当
 =x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.分两种情况:
=x时,正方形ABCD的边长为6cm,△ABE翻折后与正方形ABCD公共部分的面积y.分两种情况:①当点E在BC上时.
∵
 =x,
=x,∴
 =
= ,BE=
,BE=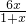 ,
,∴y=
 ×AB×BE,即y=
×AB×BE,即y=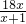 .
.②当点E在BC延长线上时,△ADF的面积为所求.
∵
 =x,∴
=x,∴ =
= ,
,又∵AD=6,
∴FC=
 ,DF=6-
,DF=6- ;
;∴
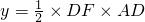 ,
,∴y=
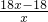 .
.分析:(1)当
 =1时,由AB∥DF,得
=1时,由AB∥DF,得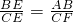 ,由AB=6,CF可求.
,由AB=6,CF可求.(2)当
 =2时,①点E在线段AB上时,延长AB′交DC于点M,求sin∠DAB′的值,即求
=2时,①点E在线段AB上时,延长AB′交DC于点M,求sin∠DAB′的值,即求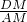 的值,由AB∥CF,可得△ABE∽△FCE,即得
的值,由AB∥CF,可得△ABE∽△FCE,即得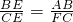 =2,又AB=6,可得CF=3;由∠BAE=∠F,又∠BAE=∠B′AE,可得∠B′AE=∠F,即MA=MF.设MA=MF=k,则MC=k-3,DM=9-k.在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,解得k=
=2,又AB=6,可得CF=3;由∠BAE=∠F,又∠BAE=∠B′AE,可得∠B′AE=∠F,即MA=MF.设MA=MF=k,则MC=k-3,DM=9-k.在Rt△ADM中,由勾股定理得:k2=(9-k)2+62,解得k= .得DM=
.得DM= ,
,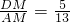 .即sin∠DAB′的值可求.②点E在不在线段AB上时,如图2所示,求sin∠DAB′的值,即是求
.即sin∠DAB′的值可求.②点E在不在线段AB上时,如图2所示,求sin∠DAB′的值,即是求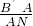 的值,同理可求.
的值,同理可求.(3)当
 =x时,求△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,同理需分两种情况,①动点的位置在线段BC上,所求△AB′E的面积即为△ABE的面积;②动点的位置不在线段BC上,△ADF的面积为所求.
=x时,求△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式,同理需分两种情况,①动点的位置在线段BC上,所求△AB′E的面积即为△ABE的面积;②动点的位置不在线段BC上,△ADF的面积为所求.点评:此题综合考查函数、正方形,平行线分线段成比例定理、图形的旋转、等知识点.分类讨论的思想,综合性强.

练习册系列答案
相关题目
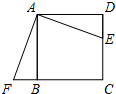 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为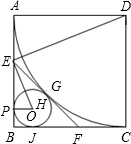 合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H
合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H (2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. (2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒.
(2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒. 如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是