题目内容
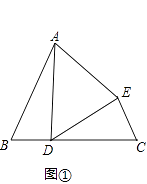
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC. 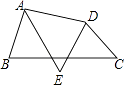
(1)如果∠B+∠C=120°,则∠AED的度数= . (直接写出结果)
(2)根据(1)的结论,猜想∠B+∠C与∠AED之间的关系,并证明.
【答案】
(1)60°
(2)解:∠AED= ![]() (∠B+∠C).
(∠B+∠C).
理由如下:在四边形ABCD中,
∵∠BAD+∠CDA+∠B+∠C=360°,
∴∠BAD+∠CDA=360°﹣(∠B+∠C),
又∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
在△AED中,又∵∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣ ![]() [360°﹣(∠B+∠C)],
[360°﹣(∠B+∠C)],
= ![]() (∠B+∠C),
(∠B+∠C),
故∠AED= ![]() (∠B+∠C).
(∠B+∠C).
【解析】解:(1)在四边形ABCD中,∵∠B+∠C=120°, ∴∠BAD+∠CDA=360°﹣120°=240°,
∵AE平分∠BAD,DE平分∠ADC,
∴∠EAD= ![]() ∠BAD,∠EDA=
∠BAD,∠EDA= ![]() ∠ADC,
∠ADC,
∴∠EAD+∠EDA= ![]() ∠BAD+
∠BAD+ ![]() ∠ADC=
∠ADC= ![]() (∠BAD+∠CDA)=
(∠BAD+∠CDA)= ![]() ×240°=120°,
×240°=120°,
在△AED中,∠AED=180°﹣(∠EAD+∠EDA),
=180°﹣120°,
=60°;
所以答案是:60°.
【考点精析】本题主要考查了多边形内角与外角的相关知识点,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目