题目内容
【题目】如图,A( ![]() ,1),B(1,
,1),B(1, ![]() ).将△AOB绕点O旋转150°得到△A′OB′,则此时点A的对应点A′的坐标为 .
).将△AOB绕点O旋转150°得到△A′OB′,则此时点A的对应点A′的坐标为 . 
【答案】(﹣1,﹣ ![]() )或(﹣2,0)
)或(﹣2,0)
【解析】解:过A作AC⊥x轴于C,∵A( ![]() ,1),
,1),
∴OC= ![]() ,AC=1,
,AC=1,
由勾股定理得:OA=2,
tan∠AOC= ![]() =
= ![]() ,
,
∴∠AOC=30°,
分两种情况:
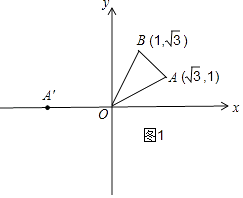
①将△AOB绕点O逆时针旋转150°得到△A′OB′,如图1,
此时OA在x轴上,则A′的坐标为(﹣2,0),
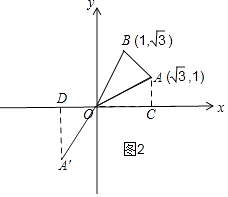
②将△AOB绕点O顺时针旋转150°得到△A′OB′,如图2,
过A′作A′D⊥x轴于D,
∵∠AOC=30°,∠AOA′=150°,
∴∠A′OC=150°﹣30°=120°,
∴∠A′OD=60°,
在Rt△A′OD中,∠DA′O=30°,A′O=2,
∴OD=1,A′D= ![]() ,
,
∴A′的坐标为(﹣1,﹣ ![]() ),
),
则点A的对应点A′的坐标为:(﹣2,0)或(﹣1,﹣ ![]() );
);
所以答案是:(﹣2,0)或(﹣1,﹣ ![]() ).
).

练习册系列答案
相关题目