题目内容
如图，正方体的棱长为4cm，M是EH的中点，现有一只蚂蚁位于点B处，它想沿正方体的表面爬行到点M处获取食物，则蚂蚁需爬行的最短路程为________cm．
2
分析：先把图中展开，根据勾股定理求出BM的长即可．
解答：
如图所示展开：连接BM，则线段BM的长就是蚂蚁需爬行的最短路程，
∵正方体的棱长为4cm，M是EH的中点，
∴∠Q=90°，BQ=（4+2）cm=6cm，
由勾股定理得：BM=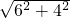
=2cm，
故答案为：2．
点评：此题考查了几何体的展开图的应用，以及线段的性质：两点之间线段最短，解决立体几何两点间的最短距离时，通常把立体图形展开成平面图形，转化成平面图形两点间的距离问题来求解．
分析：先把图中展开，根据勾股定理求出BM的长即可．
解答：
如图所示展开：连接BM，则线段BM的长就是蚂蚁需爬行的最短路程，
∵正方体的棱长为4cm，M是EH的中点，
∴∠Q=90°，BQ=（4+2）cm=6cm，
由勾股定理得：BM=
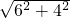=2cm，故答案为：2
．点评：此题考查了几何体的展开图的应用，以及线段的性质：两点之间线段最短，解决立体几何两点间的最短距离时，通常把立体图形展开成平面图形，转化成平面图形两点间的距离问题来求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，正方体的棱长为2，O为AD的中点，则O，A1，B三点为顶点的三角形面积为
如图，正方体的棱长为2，一只蚂蚁沿正方体的表面从A点爬到C′D′中点P的位置，则蚂蚁爬行的最短路径长为
20、如图，正方体的棱长为1米，平行光线垂直于AB，且与BC成45°角，则图中阴影部分（四边形EFGH）的面积为
如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=
如图，正方体的棱长为3，点M，N分别在CD，HE上，CM=