Question

如图，数学兴趣小组测量校园内旗杆的高度，小华拿一支刻有厘米分划的小尺，站在距旗杆30米的地方，手臂向前伸直，小尺竖直，看到尺上约12个分划恰好遮住旗杆，已知臂长60cm，则旗杆高为

 

米．

Answer 1

分析：根据题画出图形，根据相似三角形的性质解答．

解答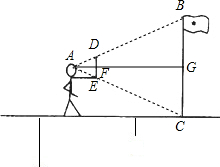：解：由题意可知△ABC是等腰三角形，AG为高，
∴BG=

1

2

BC，DF=

1

2

DE=

1

2

×12cm=0.06m，
AF为臂长，即60cm=0.6m．AG=30m，
由题意可知△AFD∽△AGB，即

AF

AG

=

DF

BG

，
即

0.6

30

=

0.06

BG

，解得BG=3m，∴BC=2BG=2×3=6m．

点评：本题考查相似三角形性质的应用．解题时关键是找出相似的三角形，然后根据对应边成比例列出方程，建立适当的数学模型来解决问题．