题目内容
如图Rt△ABC中，CD是斜边AB上的高，且AC=2BC．
求证：AD=4BD．
证明：∵Rt△ABC中，CD是斜边AB上的高，
∴△ACD∽△CBD∽△ABC．
∴
=2．
则AD=2CD，CD=2BD．
∴AD=4BD．
分析：根据Rt△ABC中，CD是斜边AB上的高，得△ACD∽△CBD∽△ABC，再根据相似三角形对应边的比相等即可证明．
点评：此题主要是相似三角形的判定和性质的综合运用．
直角三角形被斜边上的高分成的两个直角三角形和原直角三角形相似．
∴△ACD∽△CBD∽△ABC．
∴
=2．则AD=2CD，CD=2BD．
∴AD=4BD．
分析：根据Rt△ABC中，CD是斜边AB上的高，得△ACD∽△CBD∽△ABC，再根据相似三角形对应边的比相等即可证明．
点评：此题主要是相似三角形的判定和性质的综合运用．
直角三角形被斜边上的高分成的两个直角三角形和原直角三角形相似．
练习册系列答案
相关题目
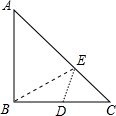如图Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为（ ）A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
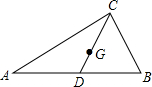如图Rt△ABC中，∠C=90°，AC=8，BC=6，CD为AB边上的中线，点G是重心，则DG=
如图Rt△ABC中，∠C=90°，AC=12cm，BC=6cm，点P从B出发，以1cm/s的速度向C运动，同时点Q从C出发，以1cm/s的速度向A运动，问几秒时PQ的长为2
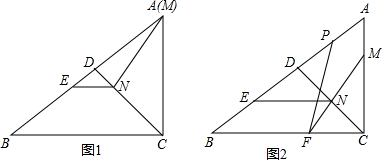
已知：如图Rt△ABC中，∠C=Rt∠，AB=5，BC=4．