题目内容
 已知如图,
已知如图, |
| AB |
| 3 |
| 1 |
| 2 |
 |
| AB |
考点:扇形面积的计算
专题:
分析:首先根据特殊角的三角函数值得出∠ABC=30°,∠AOD=60°,进而得出AC,CD,OD的长,再利用S阴影=S△ACD-S弓形AD进而得出答案.
解答: 解:连接AO,DO,AD,过点O作OE⊥AD于点E,
解:连接AO,DO,AD,过点O作OE⊥AD于点E,
∵sin∠CBA=
,∠ACB=Rt∠,
∴∠ABC=30°,
∴∠AOD=60°,
∴
=60°,
∵AO=DO,∠AOD=60°,
∴△AOD是等边三角形,
∴EO=cos30°×DO,
∵
=120°,
∴D为
的中点,
∴AD=BD,
∴∠B=∠DAB=30°,
∴∠ACD=30°,
∵AB=
,∠B=30°,
∴AC=
,
∴tan30°=
,
∴CD=
×
=
,
∴AD=1,
∴EO=
,
S弓形AD=S扇形AOD-S△AOD=
-
×
×1=
-
,
∴S阴影=S△ACD-S弓形AD=
×
×
-(
-
)=
-
.
故答案为:
-
.
 解:连接AO,DO,AD,过点O作OE⊥AD于点E,
解:连接AO,DO,AD,过点O作OE⊥AD于点E,∵sin∠CBA=
| 1 |
| 2 |
∴∠ABC=30°,
∴∠AOD=60°,
∴
 |
| AD |
∵AO=DO,∠AOD=60°,
∴△AOD是等边三角形,
∴EO=cos30°×DO,
∵
 |
| AB |
∴D为
 |
| AB |
∴AD=BD,
∴∠B=∠DAB=30°,
∴∠ACD=30°,
∵AB=
| 3 |
∴AC=
| ||
| 2 |
∴tan30°=
| CD |
| AC |
∴CD=
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
∴AD=1,
∴EO=
| ||
| 2 |
S弓形AD=S扇形AOD-S△AOD=
| 60π×12 |
| 360 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| ||
| 4 |
∴S阴影=S△ACD-S弓形AD=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| ||
| 4 |
3
| ||
| 8 |
| π |
| 6 |
故答案为:
3
| ||
| 8 |
| π |
| 6 |
点评:此题主要考查了扇形面积公式以及三角形面积求法和圆周角定理以及锐角三角函数关系等知识,得出S阴影=S△ACD-S弓形AD进而求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
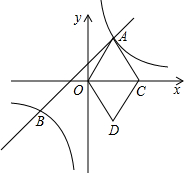 如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线
如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线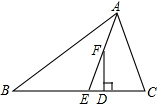 如图,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上的一点,且FD⊥BC于D,则∠EFD与∠B,∠C的关系是
如图,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上的一点,且FD⊥BC于D,则∠EFD与∠B,∠C的关系是