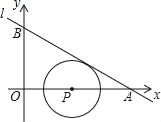
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ��
��![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() �͵�
�͵�![]() �ֱ�ӵ�
�ֱ�ӵ�![]() �͵�
�͵�![]() ͬʱ������
ͬʱ������![]() ���������˶���ͬʱ��
���������˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ������
������![]() ���������˶�����
���������˶�����![]() ��
��![]() Ϊ�ڱ߹���
Ϊ�ڱ߹���![]() ����֪��
����֪��![]() ��
��![]() ���˶��ٶȾ�Ϊ
���˶��ٶȾ�Ϊ![]() ����
����![]() ���˶��ٶ�Ϊ
���˶��ٶ�Ϊ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ������
������![]() ��������
��������![]() ��
��![]() ������һ��
������һ��![]() ����
����![]() �ڵ�
�ڵ�![]() ���Ҳࣩ��
���Ҳࣩ��![]() ���Ҹö��κ��������ֵ���䣬��Ϊ
���Ҹö��κ��������ֵ���䣬��Ϊ![]() ��
��

��1���ٵ�![]() ʱ����
ʱ����![]() �ij������ú�
�ij������ú�![]() �Ĵ���ʽ��ʾ�����ڵ�
�Ĵ���ʽ��ʾ�����ڵ�![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��2����![]() ʱ�����жϵ�
ʱ�����жϵ�![]() �Ƿ�ǡ������������
�Ƿ�ǡ������������![]() �ϣ���˵�����ɣ�
�ϣ���˵�����ɣ�
��3������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ������������
ǡ������������![]() �ϣ��������������������
�ϣ��������������������![]() ��ֵ��
��ֵ��
���𰸡���1����![]() ����
����![]() ����2�������������ϣ�����������3��1
����2�������������ϣ�����������3��1
��������
��1���ٷֱ��ʾ����P���E�����꣬���ɵõ�PE�ı���ʽ���ڵ�![]() ʱ���ɵ�E��P,D�����꣬���
ʱ���ɵ�E��P,D�����꣬���![]() ��
��![]() Ϊ�ڱ߹���
Ϊ�ڱ߹���![]() �����ʣ�������⣻
�����ʣ�������⣻
��2���������P��H�����꣬�������ߵı���ʽΪ��![]() �����ô���ϵ������������κ�������ʽ���������F�����꣬���뺯������ʽ��֤�����ɵõ����ۣ�
�����ô���ϵ������������κ�������ʽ���������F�����꣬���뺯������ʽ��֤�����ɵõ����ۣ�
��3����������κ����Ľ���ʽ��������t�����ٷ�����������ٵ�![]() ʱ���ڵ�
ʱ���ڵ�![]() ʱ���ֱ������Q�����꣬�����������t��ֵ��
ʱ���ֱ������Q�����꣬�����������t��ֵ��
��1���١ߵ�![]() ��
��![]() ���˶��ٶȾ�Ϊ
���˶��ٶȾ�Ϊ![]() ����
����![]() ���˶��ٶ�Ϊ
���˶��ٶ�Ϊ![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��
��
��P(-8+2t��0)��E(-5+t��0)��
��![]() ��
��
��-8+2t��-5+t��
��![]() ��
��
�ڡߵ�![]() ʱ��E(1��0)��P(4��0)��D(0��4)��
ʱ��E(1��0)��P(4��0)��D(0��4)��
��EP=3��OD=4��
����![]() ��
��![]() Ϊ�ڱ߹���
Ϊ�ڱ߹���![]() ����ͼ��ʾ��
����ͼ��ʾ��
��DF��EP��DF=EP=3��
��![]() ��
��
��2���ߵ�![]() ʱ��
ʱ��![]() ��
��
���![]() ����Ϊ
����Ϊ![]() ��
��
��![]() ��
��
���![]() ����Ϊ
����Ϊ![]() ��
��
�������ߵı���ʽΪ��![]() ��
��
��![]() ��
��![]() ����
����![]() ����
���� ��
��
��![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
���![]() ����Ϊ
����Ϊ![]() ��
��
�ߵ�![]() ʱ��
ʱ��![]() ��
��
���![]() ����������
����������![]() �ϣ�
�ϣ�
��3����P(-8+2t��0)��H(-2+2t��0)��
�������ߵĶԳ���Ϊ��ֱ��x=-5+2t��
�߸ö��κ��������ֵΪ![]() ��
��
��![]() ��
��
��P(-8+2t��0)����![]() ����ã�a=
����ã�a=![]() ��
��
�����![]() �������ߵı���ʽΪ��
�������ߵı���ʽΪ��![]() ��
��
�� ��![]() ʱ��
ʱ��
����PQ��FE���ӳ����ڵ�M������QE�����PME=90�㣬
��EF��PD��
���MPC=90��
��P(-8+2t��0)��D(0��-8+2t)��
��OP=OD��
���OPD=45�㣬
���MPE=45�㣬
�ɶԳ��ԣ���֪����MPE=��MQE=45�㣬PE=QE=3-t��
���PEQ=180��-45��-45��=90�㣬
��Q(-5+t��3-t)��
��![]() ǡ������������
ǡ������������![]() �ϣ�
�ϣ�
��![]() ����ã�t1=1��t2=3����ȥ����
����ã�t1=1��t2=3����ȥ����
�ڵ�![]() ʱ��
ʱ��
��P(-8+2t��0)��E(-5+t��0)��
��PE=t-3��
ͬ���ɵã���PEQ=90�㣬��MPE=��MQE=45�㣬PE=QE=t-3��
��Q�ڵ�������������ޣ�
��Q(-5+t��3-t)��
��![]() ǡ������������
ǡ������������![]() �ϣ�
�ϣ�
��![]() ����ã�t1=1����ȥ����t2=3����ȥ����
����ã�t1=1����ȥ����t2=3����ȥ����
������������![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ǡ������������
ǡ������������![]() ��ʱ��t��ֵΪ1��
��ʱ��t��ֵΪ1��




 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�����Ŀ��һ�����ѣ��˷�֧Ԯ�����¹ڷ��ס�������Ϯ������ҽ����Ա������ӧ��������ս���⣬�ڶ���ҵҲ���Ԯ��֮�֣�ij��˾�üף������ֻ������人���Ͱ������ʣ��������ص�����������±���
���ֻ������� | ���ֻ������� | �ϼ������ʶ��� | |
��һ�� | 3 | 4 | 29 |
�ڶ��� | 2 | 6 | 31 |
��1����ס������ֻ���ÿ�����طֱ���������ٶ����ʣ�
��2��Ŀǰ��46.4������Ҫ���䵽�人���ù�˾�ⰲ�ż��һ�����10����ȫ������һ�����꣬����ÿ���׳�һ�����ͻ���500Ԫ��ÿ���ҳ�һ�����ͻ���300Ԫ�����ʸù�˾Ӧ��ΰ��ų������ʡ���ã�
����Ŀ��ijӡˢ���Ĵ�ӡ��ÿ5������̭һ���ɴ�ӡ���������»������»�ʱ��ͬʱ����ī�У�ÿ��150Ԫ��ÿ̨�»���������24�У�����ͬʱ������ÿ����220Ԫ��
��˾���������ļ�¼��ʮ̨��ӡ������������������ī���������
����ī���� | 22 | 23 | 24 | 25 |
��ӡ��̨�� | 1 | 4 | 4 | 1 |
��1������ʮ̨��ӡ������ī����Ϊ���������ơ�һ��ÿ��ӡ����������5�����ĵ�ī����������24���ĸ��ʣ�
��2��������10̨��ӡ��5�����ĵ�ī������ƽ������Ϊ�������ݣ�˵������10̨�ÿ��ӡ��ʱ��ÿ̨Ӧͳһ����23��ī����24��ī�����㣿