题目内容
12、如图：AD为△ABC的高，∠B=2∠C，用轴对称图形说明：CD=AB+BD．分析：作出关于AD对称的图形，借助轴对称的性质，得到BD=DE，借助∠B=2∠C，得到AE=EC．根据题意有CD=DE+EC，将等量关系代入可得CD=DE+EC=AB+BD．
解答：
解：在CD上取一点E使DE=BD，连接AE．
可得AB与AE关于AD对称，BD=DE，
∠B=∠AED=∠C+∠EAC=2∠C，
∴∠EAC=∠C，
∴AE=EC；
则CD=DE+EC=AB+BD．
解：在CD上取一点E使DE=BD，连接AE．可得AB与AE关于AD对称，BD=DE，
∠B=∠AED=∠C+∠EAC=2∠C，
∴∠EAC=∠C，
∴AE=EC；
则CD=DE+EC=AB+BD．
点评：本题考查轴对称的性质与运用．对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
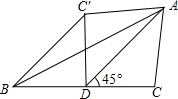如图，AD为△ABC的中线，∠ADC=45°，把△ADC沿AD对折，点C落在点C′的位置，BC=4，求BC′的长．
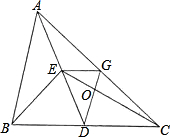如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为三角形ABD中线，
如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为△ABD的中线．