题目内容
 如图是边长为4的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
如图是边长为4的正三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标.
解:如图,以BC所在的直线为x轴,以BC边上的高所在的直线为y轴,建立平面直角坐标系,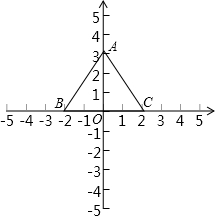
∵正三角形ABC的边长为4,
∴BO=CO=2,
∴点B、C的坐标分别为B(-2,0),C(2,0),
∵AO= =
= =2
=2 ,
,
∴点A的坐标为(0,2 ).
).
分析:以BC所在的直线为x轴,以BC边上的高所在的直线为y轴,建立平面直角坐标系,则BO=CO,再根据勾股定理求出AO的长度,点A、B、C的坐标即可写出.
点评:本题主要考查等腰三角形的性质和勾股定理的运用,建立适当的平面直角坐标系是解题的关键.

∵正三角形ABC的边长为4,
∴BO=CO=2,
∴点B、C的坐标分别为B(-2,0),C(2,0),
∵AO=
 =
= =2
=2 ,
,∴点A的坐标为(0,2
 ).
).分析:以BC所在的直线为x轴,以BC边上的高所在的直线为y轴,建立平面直角坐标系,则BO=CO,再根据勾股定理求出AO的长度,点A、B、C的坐标即可写出.
点评:本题主要考查等腰三角形的性质和勾股定理的运用,建立适当的平面直角坐标系是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.
25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心. 如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.
如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.

