Question

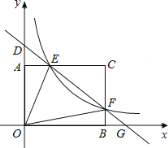
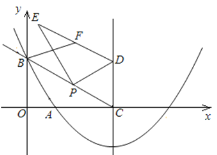
【题目】如图，在平面直角坐标系xOy中，抛物线过点，，这条抛物线的对称轴与x轴交于点C，点P为射线CB上一个动点（不与点C重合），点D为此抛物线对称轴上一点，且CPD=．

（1）求抛物线的函数表达式；

（2）若点P的横坐标为m，△PCD的面积为S，求S与m之间的函数关系式；

（3）过点P作PE⊥DP，连接DE，F为DE的中点，试求线段BF的最小值．

Answer 1

【答案】（1）；（2）（m<3）；（3）．

【解析】

试题（1）由抛物线过点，根据点在曲线上点的坐标满足方程的关系，应用待定系数法求解即可.

（2）证明△PCD是等边三角形，用m表示CP和PG，由即可求得S与m之间的函数关系式.

（3）通过证明△CPF≌△CDF得∠PCF=∠DCF，根据垂直线段最短的性质知线段BF 的最小值为点B到直线CF的距离．

（1）依题意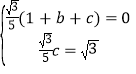，得，解得.

∴抛物线的解析式为，即．

（2）∵，∴抛物线的对称轴为．∴C（3，0）．

∵，∴．∴．

∴∠OCB=．∴∠PCD=．

∵∠CPD=，∴∠CDP=．∴△PCD是等边三角形．

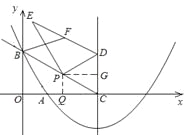
如图，过点P作PQ⊥x轴于点Q，PG∥x轴，交CD于点G，

∵点P的横坐标为m，∴OQ=m，CQ=3-m．

∴，PG=CQ=3-m．

∴，即（m<3）．

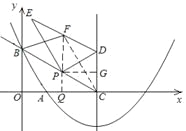
（3）如图，连接PF、CF．

∵PE⊥DP，F为DE的中点，∴PF==DF．

∵CP=CD，CF=CF，∴△CPF≌△CDF．∴∠PCF=∠DCF．

∴点F在∠PCD的平分线所在的直线上．

∴BF的最小值为点B到直线CF的距离．

∵∠OCB=∠BCF=，∴点B到直线CF的距离等于OB．

∴BF的最小值为．