题目内容

以直线为对称轴的抛物线与轴交于A、B两点,其中点A的坐标为.
（1）求点B的坐标；
（2）设点M、N在抛物线线上,且,试比较、的大小.
（1）；（2）.

试题分析：（1）根据抛物线的对称轴直接解答即可;
(2)先判断函数的增减性,再比较大小.
试题解析：(1)由已知,可得：,所以;
⑵∵∴抛物线开口向下,
∴在对称轴左侧,随的增大而增大；
∵,
∴.
练习册系列答案
相关题目
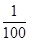某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售:①若只在国内销售,销售价格y（元/件）与月销量x（件）的函数关系式为y＝－x＋150,成本为20元/件,月利润为W内（元）;②若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件（a为常数,10≤a≤40）,当月销量为x（件）时,每月还需缴纳x2元的附加费,月利润为W外（元）．
（1）若只在国内销售,当x＝1000（件）时,y＝         （元/件）;
（2）分别求出W内、W外与x间的函数关系式（不必写x的取值范围）;
（3）若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值．
抛物线y＝ax2＋2x＋c与其对称轴相交于点A(1，4)，与x轴正半轴交于点B.
（1）求这条抛物线的函数关系式；
（2）在抛物线对称轴上确定一点C，使△ABC是等腰三角形，求出所有点C的坐标.
如图,在平面直角坐标系中,顶点为（4,1）的抛物线交轴于点,交轴于,两点（点在点的左侧）,已知点坐标为（6,0）.

（1）求此抛物线的解析式；
（2）联结AB,过点作线段的垂线交抛物线于点,如果以点为圆心的圆与抛物线的对称轴相切,先补全图形,再判断直线与⊙的位置关系并加以证明；
（3）已知点是抛物线上的一个动点,且位于,两点之间.问：当点运动到什么位置时,的面积最大？求出的最大面积.
东方商场购进一批单价为20元的日用品，销售一段时间后，经调查发现，若按每件24元的价格销售时，每月能卖36件；若按每件29元的价格销售时，每月能卖21件，假定每月销售件数y（件）与价格x（元/件）之间满足关系一次函数.
（1）试求y与x的函数关系式；
（2）为了使每月获得利润为144元，问商品应定为每件多少元？
（3）为了获得了最大的利润，商品应定为每件多少元？
天猫商城旗舰店销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%．
（1）设该旗舰店每月获得利润为w（元），求每月获得利润w（元）与销售单价x（元）之间的函数关系式，并确定自变量x的取值范围．
（2）当销售单价定为多少元时，每月可获得最大利润？每月的最大利润是多少？
（3）如果旗舰店想要每月获得的利润不低于2000元，那么每月的成本最少需要     元？
（成本＝进价×销售量）
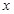根据下列表格中二次函数y＝ax2＋bx＋c的自变量与函数值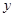的对应值,判断方程ax2＋b x＋c=0（a≠0）的一个解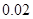的范围是（　 　）　

6．17
6．18
6．19
6．20
y＝ax2＋bx＋c
-0．03
-0．01


Ａ．6＜x＜6．17        Ｂ．6．17＜x＜6．18
Ｃ．6．18＜x＜6．19    Ｄ．6．19＜x＜6．20
将抛物线y=(x+2)2-3的图像向上平移5个单位,得到函数解析式为            ．
点A（x1,y1）、B（x2,y2）在二次函数的图象上，若x2＞x1≥m，有y2＞y1,则m的取值范围为       ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网