Question

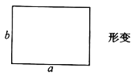
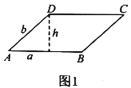
【题目】边长为，的矩形发生形变后成为边长为，的平行四边形，如图1，平行四边形中，，边上的高为，我们把与的比值叫做这个平行四边形的“形变比”．

（1）若形变后是菱形（如图2），则形变前是什么图形？

（2）若图2中菱形的“形变比”为，求菱形形变前后的面积之比；

（3）当边长为3，4的矩形变后成为一个内角是30°的平行四边形时，求这个平行四边形的“形变比”．

Answer 1

【答案】（1）正方形；（2）；（3）或．

【解析】

（１）根据形变后的图形为菱形，即可推断．

（2）由题意得形变比，再分别用代数式表示形变前和形变后的面积，计算比值即可．

（3）分以AB为底边和以AD为底边两种情况讨论，可求这个平行四边形的“形变比”．

（1）∵形变后是菱形

∴AB=BC=CD=DA

则形变前的四条边也相等

∵四条边相等的矩形是正方形

∴形变前的图形是正方形

（2）根据题意知道：

S形变前=a×b=a2

S形变后=a×h=a××a=a2

∴

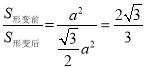
（3）当形变后四边形一个内角为30°时

此时应分两种情况讨论：

第一种：以AB为底边4×=2

∴这个四边形的形变比为：

第二种：以AD为底边

则

∴这个四边形的形变比为：．