题目内容
 如图,己知平面直角坐标系中,A(-1,3),B(2,1),线段AB交y轴于C点,求C点坐标.
如图,己知平面直角坐标系中,A(-1,3),B(2,1),线段AB交y轴于C点,求C点坐标.分析:首先过点A作AN⊥y轴于点N,过点B作BM⊥y轴于点M,得出△ANC∽BMC,进而利用A,B点的坐标得出线段长度即可得出C点坐标.
解答: 解:过点A作AN⊥y轴于点N,过点B作BM⊥y轴于点M,
解:过点A作AN⊥y轴于点N,过点B作BM⊥y轴于点M,
则∠ANC=∠BMC=90°,
∵∠ACN=∠BCM,
∴△ANC∽BMC,
∴
=
,
∵A(-1,3),B(2,1),
∴AN=1,OM=1,BM=2,
则NM=2,
∴
=
,
解得:NC=
,
∴CO=3-
=
.
∴C点坐标为:(0,
).
 解:过点A作AN⊥y轴于点N,过点B作BM⊥y轴于点M,
解:过点A作AN⊥y轴于点N,过点B作BM⊥y轴于点M,则∠ANC=∠BMC=90°,
∵∠ACN=∠BCM,
∴△ANC∽BMC,
∴
| AN |
| BM |
| NC |
| MC |
∵A(-1,3),B(2,1),
∴AN=1,OM=1,BM=2,
则NM=2,
∴
| 1 |
| 2 |
| NC |
| 2-NC |
解得:NC=
| 2 |
| 3 |
∴CO=3-
| 2 |
| 3 |
| 7 |
| 3 |
∴C点坐标为:(0,
| 7 |
| 3 |
点评:此题主要考查了相似三角形的判定与性质以及点的坐标性质,根据已知得出NC的长度是解题关键.

练习册系列答案
相关题目
 <0),作PC⊥PB交过点A的直线l于点C(4,y).
<0),作PC⊥PB交过点A的直线l于点C(4,y).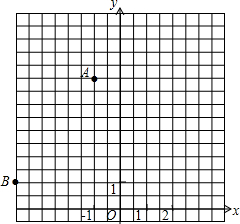 (2012•上虞市模拟)如图,已知平面直角坐标系中两点A(-1,5)、B(-4,1).
(2012•上虞市模拟)如图,已知平面直角坐标系中两点A(-1,5)、B(-4,1).
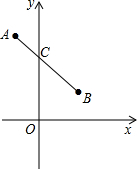 如图,己知平面直角坐标系中,A(-1,3),B(2,1),线段AB交y轴于C点,求C点坐标.
如图,己知平面直角坐标系中,A(-1,3),B(2,1),线段AB交y轴于C点,求C点坐标.