题目内容
如图,在平面直角坐标系中,直线 与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
(1)求抛物线的解析式;
(2)设点P的横坐标为m.
①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2.若存在,直接写出m的值;若不存在,请说明理由.

(1)在 中,当y=0时,x=-1;当y=5时
中,当y=0时,x=-1;当y=5时 ,x=4.
,x=4.
A(-1,0)、B(4,5) ----------------------------1分
将A(-1,0)、B(4,5)分别代入y=ax2+bx-3中,
得
解得 ,
, .
.
 ∴所求解析式为y=x2-2x-3 -------------------------3分
∴所求解析式为y=x2-2x-3 -------------------------3分
(2)①设直线AB交y轴于点E,求得E(0,1),∴OA=OE ,∠AEO=45°,
,∠AEO=45°,
∠ACP=∠AEO=45°, ∴ .
.
设 ,则
,则 ,
,
∴ . 分
. 分
∴ .
.
∴PD的最大值为 .
.
②当m=0或m=3时,PC把△PDB分成两个三角形的面积比为1:2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
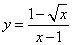 有意义的x的取值范围是 ;
有意义的x的取值范围是 ;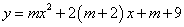 .
.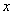 轴有两个交点,求
轴有两个交点,求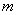 的取值范围;
的取值范围; 过,点
过,点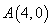 ,与
,与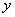 轴交于点
轴交于点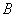 ,直线
,直线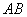 与这个二次函数图象的对称轴交于点
与这个二次函数图象的对称轴交于点 ,求点
,求点
