题目内容
(本题10分).如图,在平面直角坐标系中,一段圆弧经过格点A、B、C,其中点B坐标为(4,3).
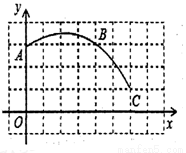
(1)请写出该圆弧所在圆的圆心D的坐标 .
(2)⊙D的半径为 ;
(3)求弧 的长(结果保留π).
的长(结果保留π).
(1)D(2,-1);(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)连接AB,BC,分别作出这两条弦的垂直平分线,两垂直平分线交于点D,即为所求圆心,由图形即可得到D的坐标;
(2)由FD=CG,AF=DG,且夹角为直角相等,利用SAS可得出三角形ADF与三角形DCG全等,由全等三角形的对应角相等得到一对角相等,再由同角的余角相等得到∠ADC为直角,利用弧长公式即可求出 的长.
的长.
试题解析:(1)连接AB,BC,分别作出AB与BC的垂直平分线,交于点D,即为圆心,由图形可得出D(2,﹣1);
(2)在Rt△AED中,AE=2,ED=4,
根据勾股定理得:AD= ;
;
(3)∵DF=CG=2,∠AFD=∠DGC=90°,AF=DG=4,
∴△AFD≌△DGC(SAS),
∴∠ADF=∠DCG,
∵∠DCG+∠CDG=90°,
∴∠ADF+∠CDG=90°,即∠ADC=90°,
则 的长l=
的长l= .
.

考点:1.垂径定理;2.坐标与图形性质;3.勾股定理;4.弧长的计算.

练习册系列答案
相关题目
 、0
、0 


 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与
),以点M为圆心,OM长为半径作⊙M .使⊙M与直线OM的另一交点为点B,与 轴、
轴、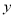 轴的另一交点分别为点D、A(如图),连接AM.点P是
轴的另一交点分别为点D、A(如图),连接AM.点P是 上的动点.
上的动点.
 ,
, ,其中a为实数,则M与N的大小关系是( )
,其中a为实数,则M与N的大小关系是( ) B.
B. C.
C. D.不能确定.
D.不能确定.