题目内容
 如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.
如图所示,在△ABC中,E为AB的中点,CD平分∠ACB,AD⊥CD于点D.试说明:(1)DE∥BC;(2)DE=
| 1 | 2 |
分析:由CD平分∠ACB,AD⊥CD于点D.可得到作辅助线方法:延长AD交BC于F点得到全等三角形.进而利用中位线知识求解.
解答: 证明:延长AD交BC于F.
证明:延长AD交BC于F.
(1)∵AD⊥CD,
∴∠ADC=∠FDC=90°.
∵CD平分∠ACB,
∴∠ACD=∠FCD.
在△ACD与△FCD中,
∠ADC=∠FDC DC=DC∠ACD=∠FCD,
∴△ACD≌△FCD.
∴AC=FC AD=DF.
又∵E为AB的中点,
∴DE∥BF,
即DE∥BC.
(2)由(1)知AC=FC,DE=
BF,
∴DE=
(BC-FC)=
(BC-AC).
 证明:延长AD交BC于F.
证明:延长AD交BC于F.(1)∵AD⊥CD,
∴∠ADC=∠FDC=90°.
∵CD平分∠ACB,
∴∠ACD=∠FCD.
在△ACD与△FCD中,
∠ADC=∠FDC DC=DC∠ACD=∠FCD,
∴△ACD≌△FCD.
∴AC=FC AD=DF.
又∵E为AB的中点,
∴DE∥BF,
即DE∥BC.
(2)由(1)知AC=FC,DE=
| 1 |
| 2 |
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了中位线定理和全等三角形的判定,解决本题的关键是作出辅助线,利用全等三角形来得出线段相等,进而应用中位线定理解决问题.

练习册系列答案
相关题目
 如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.
如图所示,在△ABC中,∠A=47°,∠C=77°,DE∥BC,BF平分∠ABC,BF交DE于点F,求∠BFE的度数.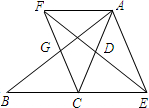 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF. 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=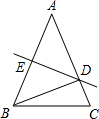 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为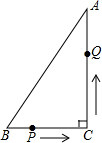 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.