题目内容
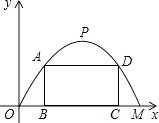
【题目】施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）． 
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A，D点在抛物线上，B，C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB，AD，DC的长度之和的最大值是多少？请你帮施工队计算一下．
【答案】
（1）解：M（12，0），P（6，6）
（2）解：∵顶点坐标（6，6）
∴设y=a（x﹣6）2+6（a≠0）
又∵图象经过（0，0）
∴0=a（0﹣6）2+6
∴ 
∴这条抛物线的函数解析式为y=﹣ 
（x﹣6）2+6，即y=﹣ x2+2x
（3）解：设A（x，y）
∴A（x，﹣ （x﹣6）2+6）
∵四边形ABCD是矩形，
∴AB=DC=﹣ （x﹣6）2+6，
根据抛物线的轴对称性，可得：OB=CM=x，
∴BC=12﹣2x，即AD=12﹣2x，
∴令L=AB+AD+DC=2[﹣ （x﹣6）2+6]+12﹣2x=﹣ 
x2+2x+12=﹣ （x﹣3）2+15．
∴当x=3，L最大值为15
∴AB、AD、DC的长度之和最大值为15米．
【解析】确定了抛物线的顶点式，可以设抛物线的顶点式，又过原点（0，0），就可以确定抛物线解析式；设OB=x，由对称性得CM=x，这样就可以用含x的式子表示AB、AD、CD了，为求三根木杆AB、AD、DC的长度之和的最大值，提供依据．
文敬图书课时先锋系列答案
【题目】为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有 人，其中选择B类的人数有 人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
【题目】自2014年12月28日北京公交地铁调价以来，人们的出行成本发生了较大的变化. 小林根据新闻，将地铁和公交车的票价绘制成了如下两个表格。（说明：表格中“6～12公里”指的是大于6公里，小于等于12公里，其他类似）
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题：
小林办了一张市政交通一卡通学生卡，目前乘坐地铁没有折扣。
（1）如果小林全程乘坐地铁的里程为14公里，用他的学生卡需要刷卡交费________元；
（2）如果小林全程乘坐公交车的里程为16公里，用他的学生卡需要刷卡交________元；
（3）小林用他的学生卡乘坐一段地铁后换乘公交车，两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元，乘坐公交车平均每公里花费0.25元，此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
