题目内容
 两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(
两建筑物AB和CD的水平距离为30米,如图所示,从A点测得太阳落山时,太阳光线AC照射到AB后的影子恰好在CD的墙角时的角度∠ACB=60°,又过一会儿,当AB的影子正好到达CD的楼顶D时的角度∠ADE=30°,DE⊥AB于E,则建筑物CD的高是多少米?(| 3 |
分析:通过投影的知识结合题意构造直角三角形,△ABC与△DCE,在这两个直角三角形中,分别求出AB、AE的长;根据ED=AB-AE=30,计算可得建筑物CD的高.
解答:解:设CD为x米.
根据题意可得:在△ABC中有:AB=BC×tan60°=
BC=30
,
在△AED中有:∠ADE=30°,AE=30
-x,
ED=
AE=
(30
-x)=30米,
解可得:x≈35,
故建筑物CD的高约是35米.
根据题意可得:在△ABC中有:AB=BC×tan60°=
| 3 |
| 3 |
在△AED中有:∠ADE=30°,AE=30
| 3 |
ED=
| 3 |
| 3 |
| 3 |
解可得:x≈35,
故建筑物CD的高约是35米.
点评:本题考查了平行投影特点:在同一时刻,不同物体的物高和影长成比例.要求学生通过投影的知识结合图形相似的性质巧妙地求解或解直角三角形,是平行投影性质在实际生活中的应用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
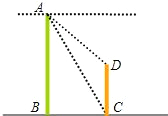 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为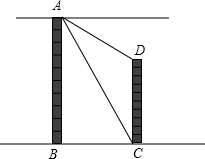 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为多少米?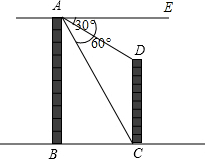 如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°.求建筑物CD的高(
如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°.求建筑物CD的高( ,结果精确到0.1米)
,结果精确到0.1米)