题目内容
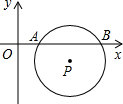
如图,平面直角坐标系中,⊙P与x轴分别交于A、B两点,点P的坐标为(3,-1),AB=2 .若将⊙P向上平移,则⊙P与x轴相切时点P坐标为
.若将⊙P向上平移,则⊙P与x轴相切时点P坐标为
- A.(3,2)
- B.(3,3)
- C.(3,4)
- D.(3,5)
A
分析:P移到P′点时,⊙P与x轴相切,过P作直径MN⊥AB与D,连接AP,由垂径定理求出AD,根据勾股定理求出AP、P′D,即可得出P′DE 坐标,即可得出答案.
解答:

当P移到P′点时,⊙P与x轴相切,
过P作直径MN⊥AB与D,连接AP,
由垂径定理得:AD=BD= AB=
AB= ,
,
∵DP=|-1|=1,
由勾股定理得:AP=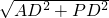 =2,
=2,
∴PP′=2+1=3,
∵P(3,-1),
∴P′的坐标是(3,2),
故选A.
点评:本题考查了垂径定理,勾股定理,切线的性质等知识点的应用,能理解题意画出图形和正确作出辅助线是解此题的关键,题目比较典型.主要培养学生的分析问题和解决问题的能力.

练习册系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.