题目内容
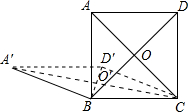 边长为2的正方形ABCD的两条对角线交于点O,把BA与CD同时分别绕点B和C逆时针方向旋转,此时正方形ABCD随之变成四边形A′BCD′,设A′C,BD′交于点O,则旋转60°时,由点O运动到点O′所经过的路径长是________.
边长为2的正方形ABCD的两条对角线交于点O,把BA与CD同时分别绕点B和C逆时针方向旋转,此时正方形ABCD随之变成四边形A′BCD′,设A′C,BD′交于点O,则旋转60°时,由点O运动到点O′所经过的路径长是________.
 π
π分析:点O以BC中点为圆心,BC的一半为半径,逆时针旋转了60度,根据弧长公式即可求得由点O运动到点O′经过的路径长为
 п.
п.解答:∵正方形ABCD的边长为2,
∴BC的一半为1
∴由点O运动到点O′经过的路径长为:
 =
= π.
π.故答案为:
 π.
π.点评:本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点-旋转中心;②旋转方向;③旋转角度.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
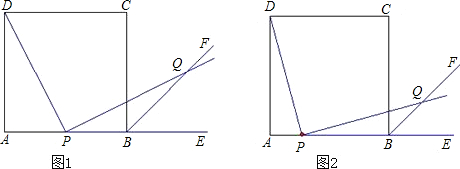


 如图,已知E是边长为12的正方形的边AB上一点,且AE=5,P是对角线AC上任意一点,则PE+PB的最小值是
如图,已知E是边长为12的正方形的边AB上一点,且AE=5,P是对角线AC上任意一点,则PE+PB的最小值是 如图,两个长方形的一部分重叠在一起,重叠部分是边长为3的正方形,则阴影部分的面积是
如图,两个长方形的一部分重叠在一起,重叠部分是边长为3的正方形,则阴影部分的面积是