题目内容
如图,在□ABCD中,AB=4cm,BC=2cm,∠B=120°,E是BC的中点,动点P从点C出发,以2cm/s的速度沿CD向终点D运动,同时动点Q从点A出发,以4cm/s的速度沿AB向终点B运动,当它们有一个到达终点时,另一个也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形AQPD为平行四边形?
(2)设DQ2=y,求y关于t的函数关系式,并写出自变量t的取值范围;
(3)在运动的过程中是否存在某一时刻,使得△CPE与△DPQ相似?若存在,请求出t的值;若不存在,请说明理由.

【答案】分析:(1)先由四边形ABCD是平行四边形可得出CD∥AB,由CD=AB=4cm,E是BC的中点可得出BC的长,欲使四边形AQPD为平行四边形,只要AQ=DP,再用t分别表示出AQ及DP的长,求出t的值即可;
(2)过点D作DF⊥AB交AB于F,在Rt△ADF中,利用锐角三角函数的定义可求出AF、DF的长,在Rt△DFQ中,由勾股定理即可得出y与t的函数关系式,根据AB=4cm,Q点的速度为4cm/s,可求出t的取值范围;
(3)先由相似三角形的判定定理得出△ADQ∽△CPE,由于两三角形相似的对应边不能确定,故应分三种情况进行讨论:
①当∠A=∠DPQ=60°时,由AB∥CD可知∠PDQ=∠AQD,再根据△ADQ∽△PDQ,AQ=DP可得出4-2t=4t,故可求出t的值;
②当∠DQP=∠A=60°时,由∠PDQ=∠AQD,△ADQ∽△PDQ,可知 ,故可得出关于t的一元二次方程,求出t的值即可;
,故可得出关于t的一元二次方程,求出t的值即可;
③当∠PDQ=∠A=60°,由∠PDQ=∠AQD=∠A=60°可知△PDQ为等边三角形,故DP=AQ=AD=2,即4-2t=2,解得t=1,而t=1时,Q已到终点,故不可能.
解答: 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=4cm,
∵E是BC的中点,BC=2cm,
∴欲使AQPD为平行四边形,只要AQ=DP.
∵动点P从点C出发,以2cm/s的速度沿CD向终点D运动,同时动点Q从点A出发,以4cm/s的速度沿AB向终点B运动,
∴AQ=4t,DP=CD-CP=4-2t,
∴4-2t=4t,
∴t= ;
;
(2)如图1,过点D作DF⊥AB交AB于F,
∵∠B=120°,AD=2cm,
∴∠A=60°,
在Rt△ADF中,
AF=ADcos60°=2×0.5=1cm
DF=ADsin60°=
在Rt△DFQ中,
DQ2= ,依题意,DQ2=y即y=16t2-8t+4,
,依题意,DQ2=y即y=16t2-8t+4,
∵AB=4cm,Q点的速度为4cm/s
∴0<t≤1;
(3)∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=4cm,
∵AD=BC=2cm,∠A=∠C=60°E为BC的中点,CP=2t,AQ=4t,
∴△ADQ∽△CPE,
①如图2,当∠A=∠DPQ=60°时,
∵AB∥CD,
∴∠PDQ=∠AQD
∵△ADQ∽△PDQ,AQ=DP
∴4-2t=4t,
∴t= ;
;
②如图3,当∠DQP=∠A=60°时,
∵∠PDQ=∠AQD, ,
,
∴DQ2=AQ•PD,即16t2-8t+4=4t(4-2t)6t2-6t+1=0,
 ,
,
 ;
;
③如图4,若∠PDQ=∠A=60°,
∵∠PDQ=∠AQD=∠A=60°
∴△PDQ为等边三角形,
∴DP=AQ=AD=2,即4-2t=2,解得t=1,
而t=1时,Q已到终点,故不可能.
综上所述,当t= 秒,
秒, 时,△PDQ∽△CPE.
时,△PDQ∽△CPE.
点评:本题考查的是相似形综合题,涉及到相似三角形的判定与性质、等边三角形的判定与性质、平行四边形的判定与性质等相关知识,难度较大.
(2)过点D作DF⊥AB交AB于F,在Rt△ADF中,利用锐角三角函数的定义可求出AF、DF的长,在Rt△DFQ中,由勾股定理即可得出y与t的函数关系式,根据AB=4cm,Q点的速度为4cm/s,可求出t的取值范围;
(3)先由相似三角形的判定定理得出△ADQ∽△CPE,由于两三角形相似的对应边不能确定,故应分三种情况进行讨论:
①当∠A=∠DPQ=60°时,由AB∥CD可知∠PDQ=∠AQD,再根据△ADQ∽△PDQ,AQ=DP可得出4-2t=4t,故可求出t的值;
②当∠DQP=∠A=60°时,由∠PDQ=∠AQD,△ADQ∽△PDQ,可知
 ,故可得出关于t的一元二次方程,求出t的值即可;
,故可得出关于t的一元二次方程,求出t的值即可;③当∠PDQ=∠A=60°,由∠PDQ=∠AQD=∠A=60°可知△PDQ为等边三角形,故DP=AQ=AD=2,即4-2t=2,解得t=1,而t=1时,Q已到终点,故不可能.
解答:
 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,∴CD∥AB,CD=AB=4cm,
∵E是BC的中点,BC=2cm,
∴欲使AQPD为平行四边形,只要AQ=DP.
∵动点P从点C出发,以2cm/s的速度沿CD向终点D运动,同时动点Q从点A出发,以4cm/s的速度沿AB向终点B运动,
∴AQ=4t,DP=CD-CP=4-2t,
∴4-2t=4t,
∴t=
 ;
;(2)如图1,过点D作DF⊥AB交AB于F,

∵∠B=120°,AD=2cm,
∴∠A=60°,
在Rt△ADF中,
AF=ADcos60°=2×0.5=1cm
DF=ADsin60°=

在Rt△DFQ中,
DQ2=
 ,依题意,DQ2=y即y=16t2-8t+4,
,依题意,DQ2=y即y=16t2-8t+4,∵AB=4cm,Q点的速度为4cm/s
∴0<t≤1;
(3)∵四边形ABCD是平行四边形,
∴CD∥AB,CD=AB=4cm,
∵AD=BC=2cm,∠A=∠C=60°E为BC的中点,CP=2t,AQ=4t,

∴△ADQ∽△CPE,
①如图2,当∠A=∠DPQ=60°时,
∵AB∥CD,

∴∠PDQ=∠AQD
∵△ADQ∽△PDQ,AQ=DP
∴4-2t=4t,
∴t=
 ;
;②如图3,当∠DQP=∠A=60°时,
∵∠PDQ=∠AQD,
 ,
,∴DQ2=AQ•PD,即16t2-8t+4=4t(4-2t)6t2-6t+1=0,
 ,
, ;
;
③如图4,若∠PDQ=∠A=60°,
∵∠PDQ=∠AQD=∠A=60°
∴△PDQ为等边三角形,
∴DP=AQ=AD=2,即4-2t=2,解得t=1,
而t=1时,Q已到终点,故不可能.
综上所述,当t=
 秒,
秒, 时,△PDQ∽△CPE.
时,△PDQ∽△CPE.点评:本题考查的是相似形综合题,涉及到相似三角形的判定与性质、等边三角形的判定与性质、平行四边形的判定与性质等相关知识,难度较大.

练习册系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=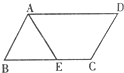 18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
18、如图,在?ABCD中,∠A的平分线交BC于点E,若AB=10cm,AD=14cm,则EC=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.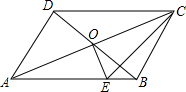 如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是
如图,在?ABCD中,∠ADB=90°,CA=10,DB=6,OE⊥AC于点O,连接CE,则△CBE的周长是