题目内容
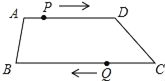
【题目】如图，∠AOB=90°，OA=90cm，OB=30cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少?
【答案】50cm
【解析】
试题分析：根据小球滚动的速度与机器人行走的速度相等得出BC=AC，设BC=AC=xcm，从而得出OC=（90－x）cm，然后根据Rt△BOC的勾股定理得出方程，从而求出x的值．
试题解析：∵小球滚动的速度与机器人行走的速度相等 ∴BC=AC
设BC=AC=xcm ∴OC=（90－x）cm 在Rt△BOC中，
∴
解得：x=50
答：机器人行走的路程BC为50cm．
练习册系列答案
相关题目
【题目】某学校兴趣小组，对函数y＝|x﹣1|+1的图像和性质进行了研究，探究过程如下：
（1）自变量
的取值范围是全体实数，
与的几组对应值如表：
X | …… |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | …… |
其中
（2）在平面直角坐标系中，画出上表中对应值为点的坐标，根据画出的点，画出该函数的图象；
（3）根据画出的函数图像特征，仿照示例，完成下表中函数的变化规律：
序号 | 函数图像特征 | 函数变化规律 |
示例1 | 在直线 | 当 |
① | 在直线 |
|
示例2 | 函数图像经过点（-3，5） | 当 |
② | 函数图像的最低点是 | 当 |
（4）当
时，的取值范围是_____________
