题目内容
已知二次函数y=(n-1)x2+2mx+1图象的顶点在x轴上,
(1)试判断这个二次函数图象的开口方向,并说明你的理由;
(2)求证:函数y=m2x2+2(n-1)x-1的图象与x轴必有两个不同的交点.
解:(1)∵二次函数y=(n-1)x2+2mx+1图象的顶点在x轴上,
∴函数顶点的纵坐标为0,
∴ =
=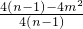 =0,
=0,
∴4(n-1)-4m2=0,
∴(n-1)=m2≥0,
∴函数开口方向向上;
(2)∵函数顶点的纵坐标为0,
∴4(n-1)=4m2,
∵△=(2n-2)2-4m2(-1)=4(n-1)2+4m2=4m4+4m2,
∴△>0,
∴函数y=m2x2+2(n-1)x-1的图象与x轴必有两个不同的交点.
分析:(1)根据函数的顶点坐标在x轴上,可以知函数顶点的纵坐标为0,然后求出(n-1)的范围,从而求解.
(2)已知函数的解析式为y=m2x2+2(n-1)x-1,根据判别式△与0的关系,来判断函数与x轴交点的个数.
点评:(1)第一问主要考查函数的基本性质及顶点坐标公式,函数开口的方向,比较简单;
(2)第二问主要利用根的判别式来求解,要利用第一问的结论,计算要仔细.
∴函数顶点的纵坐标为0,
∴
 =
=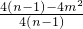 =0,
=0,∴4(n-1)-4m2=0,
∴(n-1)=m2≥0,
∴函数开口方向向上;
(2)∵函数顶点的纵坐标为0,
∴4(n-1)=4m2,
∵△=(2n-2)2-4m2(-1)=4(n-1)2+4m2=4m4+4m2,
∴△>0,
∴函数y=m2x2+2(n-1)x-1的图象与x轴必有两个不同的交点.
分析:(1)根据函数的顶点坐标在x轴上,可以知函数顶点的纵坐标为0,然后求出(n-1)的范围,从而求解.
(2)已知函数的解析式为y=m2x2+2(n-1)x-1,根据判别式△与0的关系,来判断函数与x轴交点的个数.
点评:(1)第一问主要考查函数的基本性质及顶点坐标公式,函数开口的方向,比较简单;
(2)第二问主要利用根的判别式来求解,要利用第一问的结论,计算要仔细.

练习册系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;