题目内容
在△OAB中,O为坐标原点,横、纵轴的单位长度相同,A、B的坐标分别为(8,6),(16,0),点P沿OA边从点O开始向终点A运动,速度每秒1个单位,点Q沿BO边从B点开始向终点O运动,速度每秒2个单位,如果P、Q同时出发,用t(秒)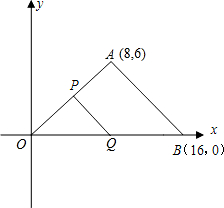 表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动.
表示移动时间,当这两点中有一点到达自己的终点时,另一点也停止运动.
求:(1)几秒时PQ∥AB;
(2)设△OPQ的面积为y,求y与t的函数关系式;
(3)△OPQ与△OAB能否相似?若能,求出点P的坐标,若不能,试说明理由.
 解:(1)由已知得
解:(1)由已知得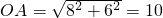 ,
,当PQ∥AB时,
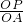 =
=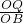 ,
,则:
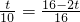 ,得:
,得:
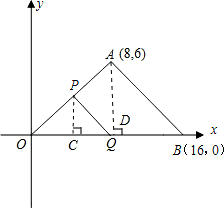
(2)过P作PC⊥OB,垂足为C,过A作AD⊥OB,垂足为D.则
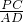 =
=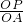 ,
,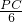 =
= ,
,∴PC=
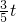 ,y=
,y= OQ•PC=
OQ•PC= (16-2t)•
(16-2t)• t=-
t=-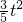 +
+ t;
t;∴y=-
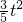 +
+ t;
t;(3)能相似.
①若PQ∥AB,∴∠OAB=∠OPQ,∠ABO=∠PQO,
∴△OPQ∽△OAB,
∵t=
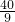 ,∴OP=
,∴OP=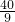 ,
,∵
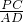 =
=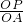 =
= (其中AD=6,OA=10,OD=8)即
(其中AD=6,OA=10,OD=8)即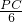 =
=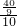 =
=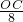 ,
,∴OC=
 ,PC=
,PC= ,
,∴P点坐标是(
 ,
, ).
).同理,当OPQ∽△OBA时,OC=
 ,PC=
,PC=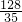
∴P2(
 ,
,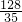 )
)P点的坐标是(
 ,
, )或(
)或( ,
,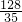 )
)分析:(1)由两点间的距离公式求得AO=10,然后根据平行线PQ∥AB分线段成比例知
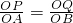 ,据此列出关于t的方程,并解方程;
,据此列出关于t的方程,并解方程;(2)过P作PC⊥OB,垂足为C,过A作AD⊥OB,垂足为D.构造平行线PC∥AQ,根据平行线分线段成比例及三角形的面积公式求得关于y与t的函数关系式;
(3)当PQ∥AB时,得到两对同位角相等,利用两对对应角相等的两三角形相似可得△OPQ∽△OAB.然后根据相似三角形的性质:对应线段成比例求得点P的坐标.
点评:本题综合考查了相似三角形的判定与性质、平行线分线段成比例及勾股定理的应用.解答此题的关键是通过作辅助线PC⊥OB,AD⊥OB构造平行线PC∥AQ,然后利用平行线分线段成比例来求出相关线段的长度.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.
已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标. 已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.
已知,如图:点A(1,1),点B在坐轴上,试以OA为边,使三角形OAB为等腰三角形,试在图中画这个等腰三角形并求点B的坐标.