题目内容
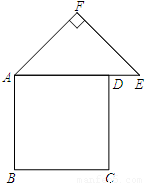
如图，有一张纸片，是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的（b＜a），∠AFE=90°，且边AD和AE在同一条直线上．要通过适当的剪拼，得到一个与之面积相等的正方形．（Ⅰ）该正方形的边长为 ；
（Ⅱ）现要求只能用两条裁剪线，请你设计一种裁剪的方法，在图中画出裁剪线，并简要
说明剪拼的过程： ．
【答案】分析：（Ⅰ）先求出正方形ABCD的面积与等腰直角三角形的面积的和，然后根据正方形的面积等于边长的平方解答；
（Ⅱ）根据勾股定理在正方形ABCD的边AB上截取BG=b，然后连接CG、FG并延其剪开，再以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置即可得到新正方形．
解答：解：（Ⅰ）∵正方形ABCD的边长为a，等腰直角三角形FAE的斜边为2b，
∴所得新正方形的面积为a2+
×2b×b=a2+b2，
∴新正方形的边长为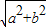
；
（Ⅱ）如图，
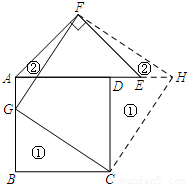
①在BA上截取BG=b；
②画出两条裁剪线CGFG；
③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．
此时，得到的四边形FGCH即为所求．
点评：本题考查了图形的剪拼，（Ⅰ）根据剪拼前后图形的面积相等是求出新正方形边长的关键，（Ⅱ）利用勾股定理确定出新正方形的边长确定出出点G是确定裁剪线的关键，也是本题的难点．
（Ⅱ）根据勾股定理在正方形ABCD的边AB上截取BG=b，然后连接CG、FG并延其剪开，再以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置即可得到新正方形．
解答：解：（Ⅰ）∵正方形ABCD的边长为a，等腰直角三角形FAE的斜边为2b，
∴所得新正方形的面积为a2+
×2b×b=a2+b2，∴新正方形的边长为
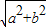；（Ⅱ）如图，
①在BA上截取BG=b；
②画出两条裁剪线CGFG；
③以点C为旋转中心，把△CBG顺时针旋转90°到△CDH的位置，以点F为旋转中心，把△FAG逆时针旋转90°到△FEH的位置．
此时，得到的四边形FGCH即为所求．
点评：本题考查了图形的剪拼，（Ⅰ）根据剪拼前后图形的面积相等是求出新正方形边长的关键，（Ⅱ）利用勾股定理确定出新正方形的边长确定出出点G是确定裁剪线的关键，也是本题的难点．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
NM与梯形BCNM的重叠面积为S，
（2013•吉安模拟）如图，有一张矩形纸片ABCD，已知AB=2，BC=4，若点E是AD上的一个动点（与点A不重合），且0＜AE≤2，沿BE将△ABE对折后，点A落到点P处，连接PC．
（2013•深圳）如图，有一张一个角为30°，最小边长为2的直角三角形纸片，沿图中所示的中位线剪开后，将两部分拼成一个四边形，所得四边形的周长是（ ）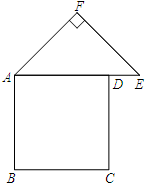
（2012•和平区一模）如图，有一张纸片，是由边长为a的正方形ABCD、斜边长为2b的等腰直角三角形FAE组成的（b＜a），∠AFE=90°，且边AD和AE在同一条直线上．要通过适当的剪拼，得到一个与之面积相等的正方形．