题目内容
(本小题满分10分)如图,AB是⊙O直径,D为⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C.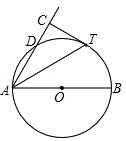
(1)求证:CT为⊙O的切线;
(2)若⊙O半径为2,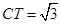 ,求AD的长.
,求AD的长.
(1)证明:连接OT,
∵OA=OT,
∴∠OAT=∠OTA,
又∵AT平分∠BAD,
∴∠DAT=∠OAT,
∴∠DAT=∠OTA,
∴OT∥AC,
又∵CT⊥AC,
∴CT⊥OT,
∴CT为⊙O的切线
(2)解:过O作OE⊥AD于E,则E为AD中点,
又∵CT⊥AC,
∴OE∥CT,
∴四边形OTCE为矩形
∵CT= ,
,
∴OE= ,
,
又∵OA=2,
∴在Rt△OAE中, ,
,
∴AD=2AE=2
解析试题分析:(1)连接OT,根据角平分线的性质,以及直角三角形的两个锐角互余,证得CT⊥OT,CT为⊙O的切线;
(2)证明四边形OTCE为矩形,求得OE的长,在直角△OAE中,利用勾股定理即可求解
考点:切线的判定与性质;勾股定理;圆周角定理
点评:本题主要考查了切线的判定以及性质,证明切线时可以利用切线的判定定理把问题转化为证明垂直的问题

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
如图,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( )
| A.1 | B. | C.2 | D. |
下列说法中,正确的是( )
| A.长度相等的两条弧是等弧 |
| B.优弧一定大于劣弧 |
| C.不同的圆中不可能有相等的弦 |
| D.直径是弦且是同一个圆中最长的弦 |
 +3=0是关于x的一元一次方程,则m的值是 .
+3=0是关于x的一元一次方程,则m的值是 .



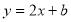 经过点A(1,3),与y轴交于点B,与x轴交于点C.
经过点A(1,3),与y轴交于点B,与x轴交于点C.